本文介绍ctc算法1。之前有了解过大致细节,发现还是很容易忘记。还是需要自己啃一下论文。以下是论文笔记。有一些疑问,待看了源码再做补充。
介绍
ctc用在语音识别,取得不错的效果。最近学术界以及我自己在ocr的实践也证明了其可行性。
语音识别
对于传统的语音识别来说,一般需要先对语音进行分帧处理。每帧10ms。一般需要使用”强制对齐“的方式,使得语音和标签一一对应,然后再训练这个预测关系。
这样预测是前后文独立的,这个对齐结果对最后结果也会有较大影响。
ocr
传统的文字识别一般分为检测,分割,识别三个步骤。先检测到文字位置,再将每个文字切割出来,放到svm等分类器进行分类。但分割本身是非常麻烦的问题。对于手写字有黏连的情况,或者验证码这种故意扭曲的图片,很难有很好的结果。
基于ctc的文字识别就是直接把整张图片和对应的文本标签扔进来,由算法学习里面的对齐关系。并按照概率最大,输出对应的标签。
下文主要以ctc在语音识别上的应用进行举例。改天再专门介绍ctc在ocr上的应用实例。
工作原理

以上图片来自这篇一篇很好的博客2。
我们先用上面这张图来说明ctc的基本工作原理。第一行是输入的波形。第二行是分帧预测结果。第三行是对结果进行合并。合并规则如下:
- 合并相同的标签
- 去除blank符号
blank符号用于表示一种犹豫不定的状态。后文用$\epsilon$ 表示。
那么大家可能心里就会问,多了一个$\epsilon$有啥特殊的吗?跟分帧预测有什么区别吗?
我们先来看一张图。在这张图中,可以看到ctc预测结果和分帧有明显的不同。

上图第一行是波形,第二行是分帧预测结果,第三行是ctc的结果。(岂不是说,使用ctc很难准确获取每个音素的起始结束时间?待确定todo)
从上图可以看到对于分帧预测来说,需要在一个音素持续的时间内,持续地保持该音素是最大的概率。如果不是,则会导致最后结果不对。(当然,可以通过语言模型进行修正)
而最后一行的ctc预测则完全不一样。在整个预测过程大部分时间都是blank状态,在少数位置上输出对应的音素。与rnn进行结合,有前后文信息,进一步提高预测的准确性。
预测
ctc其实是一种损失函数。在预测的时候,可以使用跟分帧完全一样的方式进行处理。
符号
为了方便表达,我们先引入一些符号。
- $L$: 原来的标签集合
- $L’$: 原本的标签 + blank
- $y_k^t$: 第$t$帧是$k$标签的观测概率
- $\pi$: 路径
- $\mathcal{B}$: 用来表示多对一映射。比如说: $\mathcal{B}(a-ab-)=\mathcal{B}(-aa—abb)=aab$
那么:
\[p({\mathbf l}\mid x)=\sum_{\pi\in \mathcal{B}^{-1}({\mathbf l})}p(\pi \mid x) \qquad(1)\]上式的意思是,对于给定输入$x$, 输出${\mathbf l}$的概率是:所有可能通过$\mathcal{B}$映射而获得${\mathbf l}$的路径$\pi$的概率和。
一听到路径概率和,有没有一种冲动:用vertebi算法 :)。额,这里用不了。与hmm和crf不同,这里没有转移概率。
这里比较复杂的是有个映射。通常使用prefix search(待细化)来搞。但比较耗时。也有按照高于一定阈值的blank来划分成多个段来减少耗时。
常用的方法就是直接取每个位置最大概率的标签。
那么现在剩下的问题就是训练了。
训练
前向后向
训练使用前向后向算法。(可以先复习一下hmm的前向后向训练,对于理解ctc有帮助。)
$\alpha_t(s)$表示在第$t$帧,前面的预测序列是$\mathbf{l}_{1:s}$的概率。
\[a_t(s)=\sum_{\pi \in N^T, \mathcal{B}({\pi_{1:t})=\mathbf{l}_{1:s}}}\prod_{t'=1}^ty_{\pi_{t'}}^{t'}\]后面我们会看到,$\alpha_t(s)$可以表示成$\alpha_{t-1}(s)$和$\alpha_{t-1}(s-1)$. 从而大大节约计算量。
在训练的时候会将标签从$\mathbf{l}$改成$\mathbf{l}’$。主要是在每个标签之间插入blank。使得总长度是$2\mid\mathbf{l} \mid +1$.
如下图所示,横向表示时间帧。纵向表示标签序列(白色是blank,黑色是正常标签)。cat的概率是所有可能路径之和。
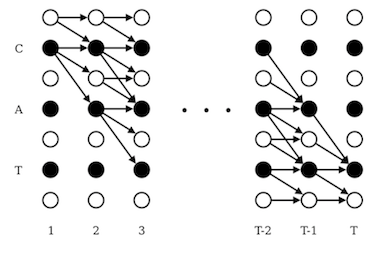
对于一个序列,可以从blank开始,也可以用正确的标签开始,所以有以下初始条件:
- $\alpha_1(1)=y_\epsilon^1$
- $\alpha_1(2)=y_{\mathbf{l}_1}^1$
- $\alpha_1(s)=0, \forall s>2$
其中 \(\bar{\alpha}_t(s)=\alpha_{t-1}(s)+\alpha_{t-1}(s-1)\)
解释一下为什么这里需要分这两种情况考虑。
比如对于abb这样的序列,对应的$\mathbf{l’}$是: -a-b-b-
- 第一种情况
- 在预测到$\epsilon$的时候,必须保证前面一个是$\epsilon$或者前面已经是正确的标签了
- 预测第二个b的时候,必须保证前面一个是$\epsilon$或者b
- 第二种情况
- 在预测第一个b时,前面一个是$a,b,\epsilon$都是可以的。
同理或者后向 $\beta_t^s$
最大似然训练
\[p(\mathbf{l}\mid x)=\sum_{s=1}^{\mid \mathbf{l}' \mid}\frac{\alpha_t(s)\beta_t(s)}{y_{\mathbf{l}'_s}^t}\]对于$y_k^t$,只需要考虑标签$k$就可以了。
因为会有重复,所以我们需要几下标签$k$出现的位置(todo:论文这里没有说清楚这个k指的是当前这个k,还是所有跟k相同标签的位置。回头看下mxnet ctc代码再做补充):
\[lab(\mathbf{l}, k)=\{s : \mathbf{l}'_s = k\}\]与hmm的区别
hmm的训练参考之前的文章. 待补充
mxnet ctc 实现
todo
参考文献: