结合代码谈谈最大熵
吴军数学之美:
说白了,就是要保留全部的不确定性,将风险降到最小。最 大熵原理指出,当我们需要对一个随机事件的概率分布进行预测时,我们的预测应当满足全部已知的条件,而对未知的情况不要做任何主观假设。(不做主观假设这 点很重要。)在这种情况下,概率分布最均匀,预测的风险最小。因为这时概率分布的信息熵最大,所以人们称这种模型叫”最大熵模型”。
例子代码参考博文
基于最大熵的中文分词参考这里
#!/usr/bin/python
#coding=utf8
import sys;
import math;
from collections import defaultdict
class MaxEnt:
def __init__(self):
self._samples = []; #样本集, 元素是[y,x1,x2,...,xn]的元组
self._Y = set([]); #标签集合,相当于去重之后的y
self._numXY = defaultdict(int); #Key是(xi,yi)对,Value是count(xi,yi)
self._N = 0; #样本数量
self._n = 0; #特征对(xi,yi)总数量
self._xyID = {}; #对(x,y)对做的顺序编号(ID), Key是(xi,yi)对,Value是ID
self._C = 0; #样本最大的特征数量,用于求参数时的迭代,见IIS原理说明
self._ep_ = []; #样本分布的特征期望值
self._ep = []; #模型分布的特征期望值
self._w = []; #对应n个特征的权值
self._lastw = []; #上一轮迭代的权值
self._EPS = 0.01; #判断是否收敛的阈值
def load_data(self, filename):
for line in open(filename, "r"):
sample = line.strip().split();
print len(sample)
if len(sample) < 2: #至少:标签+一个特征
continue;
y = sample[0];
X = sample[1:];
self._samples.append(sample); #labe + features
self._Y.add(y); #label
for x in set(X): #set给X去重
print x,y
self._numXY[(x, y)] += 1;
def _initparams(self):
self._N = len(self._samples);
self._n = len(self._numXY);
self._C = max([len(sample) - 1 for sample in self._samples]);
self._w = [0.0] * self._n;
self._lastw = self._w[:];
self._sample_ep();
def _convergence(self):
for w, lw in zip(self._w, self._lastw):
if math.fabs(w - lw) >= self._EPS:
return False;
return True;
def _sample_ep(self):
self._ep_ = [0.0] * self._n;
#计算方法参见公式(20)
for i, xy in enumerate(self._numXY):
self._ep_[i] = self._numXY[xy] * 1.0 / self._N;
self._xyID[xy] = i;
def _zx(self, X): # X=['rainy','mild','high','FALSE']
#calculate Z(X), 计算方法参见公式(15)
ZX = 0.0;
for y in self._Y:
sum = 0.0;
for x in X:
if (x, y) in self._numXY:
sum += self._w[self._xyID[(x, y)]];
ZX += math.exp(sum);
return ZX;
def _pyx(self, X):
#calculate p(y|x), 计算方法参见公式(22)
ZX = self._zx(X);
results = [];
for y in self._Y:
sum = 0.0;
for x in X:
if (x, y) in self._numXY: #这个判断相当于指示函数的作用
sum += self._w[self._xyID[(x, y)]];
pyx = 1.0 / ZX * math.exp(sum);
results.append((y, pyx));
return results;
def _model_ep(self):
self._ep = [0.0] * self._n;
#参见公式(21)
for sample in self._samples:
X = sample[1:];
pyx = self._pyx(X);
for y, p in pyx:
for x in X:
if (x, y) in self._numXY:
self._ep[self._xyID[(x, y)]] += p * 1.0 / self._N;
def train(self, maxiter = 1000):
self._initparams();
for i in range(0, maxiter):
print "Iter:%d..."%i;
self._lastw = self._w[:]; #保存上一轮权值
self._model_ep();
#更新每个特征的权值
for i, w in enumerate(self._w):
#参考公式(19)
self._w[i] += 1.0 / self._C * math.log(self._ep_[i] / self._ep[i]);
print self._w;
#检查是否收敛
if self._convergence():
break;
def predict(self, input):
X = input.strip().split("\t");
prob = self._pyx(X)
return prob;
if __name__ == "__main__":
maxent = MaxEnt();
maxent.load_data('data.txt');
maxent.train();
print maxent.predict("sunny\thot\thigh\tFALSE");
print maxent.predict("overcast\thot\thigh\tFALSE");
print maxent.predict("sunny\tcool\thigh\tTRUE");
sys.exit(0);
上面用到的公式:

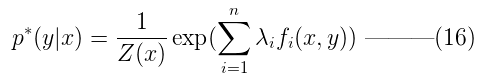
通过求对偶问题内部问题的极小化,将原约束最大化问题转化为公式16的最大化问题。接下来要求解的是,使得公式16最大化的权值。

其中data.txt是根据天气情况决定是否去打球。第一列是是否打球,后面列是特征。
no sunny hot high FALSE
no sunny hot high TRUE
yes overcast hot high FALSE
yes rainy mild high FALSE
yes rainy cool normal FALSE
no rainy cool normal TRUE
yes overcast cool normal TRUE
no sunny mild high FALSE
yes sunny cool normal FALSE
yes rainy mild normal FALSE
yes sunny mild normal TRUE
yes overcast mild high TRUE
yes overcast hot normal FALSE
no rainy mild high TRUE
最原始的最大熵模型的训练方法是一种称为通用迭代算法 GIS(generalized iterative scaling) 的迭代算法。GIS 的原理并不复杂,大致可以概括为以下几个步骤[来自数学之美]:
- 假定第零次迭代的初始模型为等概率的均匀分布。
- 用第 N 次迭代的模型来估算每种信息特征在训练数据中的分布,如果超过了实际的,就把相应的模型参数变小;否则,将它们便大。
- 重复步骤 2 直到收敛。
在这个例子中,将X的所有可能取值和y的取值进行组合,获得关于(x,y)的统计信息。直接的统计信息是_sample_ep。并将结果保存在self.ep(对应于公式20)。 而在训练时候,_model_ep,要使参数self._ep(对应于公式21)与统计信息一致。根据两者之间的差别,对权值进行调整。直到收敛。
在实际训练中,最大熵的计算量非常大。GIS算法不稳定,即使用其改进版的迭代尺度算法也很慢。在统计学习方法中还介绍了拟牛顿法等。