glove词向量。GloVe: Global Vectors for Word Representation
词向量是什么
自然语言理解的问题要转化为机器学习的问题,第一步肯定是要找一种方法把这些符号数学化。
NLP 中最直观,也是到目前为止最常用的词表示方法是 One-hot Representation,这种方法把每个词表示为一个很长的向量。
这个向量的维度是词表大小,其中绝大多数元素为 0,只有一个维度的值为 1,这个维度就代表了当前的词。
举个栗子,
“话筒”表示为 [0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 …]
“麦克”表示为 [0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 …]
每个词都是茫茫 0 海中的一个 1。
这种 One-hot Representation 如果采用稀疏方式存储,会是非常的简洁:也就是给每个词分配一个数字 ID。
比如刚才的例子中,话筒记为 3,麦克记为 8(假设从 0 开始记)。如果要编程实现的话,用 Hash 表给每个词分配一个编号就可以了。
这么简洁的表示方法配合上最大熵、SVM、CRF 等等算法已经很好地完成了 NLP 领域的各种主流任务。
当然这种表示方法也存在一个重要的问题就是“词汇鸿沟”现象:任意两个词之间都是孤立的。
光从这两个向量中看不出两个词是否有关系,哪怕是话筒和麦克这样的同义词也不能幸免于难。
Deep Learning 中一般用到的词向量并不是刚才提到的用 One-hot Representation 表示的那种很长很长的词向量
,而是用 Distributed Representation(不知道这个应该怎么翻译,因为还存在一种叫“Distributional Representation”的表示方法,
又是另一个不同的概念)表示的一种低维实数向量。这种向量一般长成这个样子:[0.792, −0.177, −0.107, 0.109, −0.542, …]。
维度以 50 维和 100 维比较常见。这种向量的表示不是唯一的,后文会提到目前计算出这种向量的主流方法。
以上文字来自:词向量和语言模型
Distributed representation 用来表示词,通常被称为“Word Representation”或“Word Embedding”(词嵌入)。其中最出名的是word2vec。
Glove是stanford nlp组出品,效果比word2vec更好。
词向量作用
词向量用来获得线性关系和相似性问题.
1 线性关系
最出名的例子是:
man - woman = king - queen
同样可以用来解决:
中国 - 北京 = 法国 - 巴黎
2 相似性

这个例子中输入搜索词:frog。输出以及相近的词汇。从右边的图片可以看出,其获取相似性效果非常好。
GloVe原理
在这个例子中,我们要考察的是,ice和steam的关系。这两个词的分别对应于\(i\)和\(j\). 同时,我们希望通过单词共现来获取它们之间的关系。\(i\)和\(j\)在其上下文窗口中,出现的单词记为\(k\)。我们希望通过\(k\)来获取\(i\)和\(j\)的关系。在这个例子中,\(i=ice\),\(j=steam\), \(k=solid,gas,water,fashion\) 等。其中\(P(k=gas\mid ice)=\frac{P(gas,ice)}{P(ice)}=\frac{P_{ik}}{P_i}\).
在\(i,j\)有区分的维度 \(\frac{P_{ik}}{P_{jk}}\) 要么很大,要么很小。比如,上面的\(8.9\)和\(8.5x10^{-2}\).其他的值都会很接近于1.
公式推导
\[F(w_i,w_j, \tilde{w_k})=\frac{P_{ik}}{P_{jk}}\qquad(1)\]其中\(w_i\)是词向量(word vector),\(\tilde{w_k}\)是上下文词向量(context word vector)。 为了表示内在的线性关系,使用差分进行表示:
\[F(w_i-w_j, \tilde{w_k})=\frac{P_{ik}}{P_{jk}}\qquad(2)\]上面公式的左边是向量,右边是标量。可以通过神经网络等算法来学习这个\(F\)参数(实际上真的有文章是这么做的)。但是这样做,会使得我们想获得的线性关系变得模糊。为了避免这个问题,使用点乘进行表示: \(F((w_i-w_j)^T\tilde{w_k})=\frac{P_{ik}}{P_{jk}}\qquad(3)\)
所谓的上下文词向量跟词向量本身很难界定关系,甚至可以互相替换。也就是\(w\)和\(\tilde{w}\)也可以相互交换的。但是公式(3)不行。所以,作者要求\(F\)必须是同质(homomorphism)的,即: \(F((w_i-w_j)^T\tilde{w_k})=\frac{F(w_i^T\tilde{w_k})}{F(w_j^T\tilde{w_k})}\qquad(4)\)
由公式(3)可得,
\[F(w_i^T\tilde{w_k})=P_{ik}=\frac{X_{ik}}{X_i} \qquad(5)\]公式(4)的解是, \(F=exp\),或者,
\[w_i^T\tilde{w_k}=log(X_{ik})-log(X_i) \qquad(6)\]其中\(log(X_i)\)独立于\(k\),所以,该项可以放都\(w_i\)的偏置项\(b_i\)中。所以,
\[w_i^T\tilde{w_k}+b_i+\tilde{b_k}=log(X_{ik}) \qquad(7)\]现在还存在一个问题:所以词的权重都是一样的。而实际上,我们希望很少出现(可能是噪声),或者经常出现(可能是功能词)的权重不要太大。在公式(7)的基础上引入权重\(f(X_{ij})\):
\[J=\sum_{i,j=1}^{V}f(X_{ij})(w_i^T\tilde{w_k}+b_i+\tilde{b_k}-log(X_{ik}))^2 \qquad(8)\]通过作者的实验,
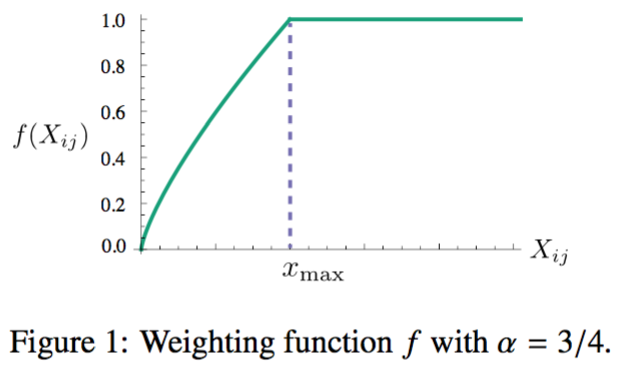
\[f(x) = \begin{cases} (x/x_{max})^a & \text{if $x<x_{max}$ } \\ 1 & \text{otherwise} \end{cases} \qquad(9)\]其中\(x_{max}=100\), \(\alpha=0.75\)取得很好的效果。
源码笔记
代码写得很漂亮高效,值得学习
vocab_count.c
统计输入文件单词出现频率,并按单词频率从大到小的字母顺序排列 实现了hash函数等:
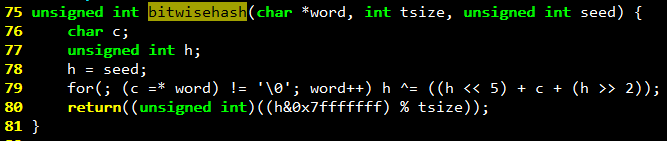
cooccur.c
cooccur的基本思路是记录每个单词与其他单词一起出现的概率
主要是外存堆排序
lookup是个累计函数。lookup[a]保存在词频上排行为a的词在bigram_table上的起始下标。
在bigram_table上每个单词的保存数目分别为:max_product / a; 对于部分贡献单词数目超出部分,先保存在缓存数组中,缓存数组满,则写入文件。假设最终写到k个文件中
遍历完token(单词)之后,将biggram_table写入到第k+1个文件中。对于每行,内容为word1, word2, weight;这里weight需要将两者在窗口内的距离计算在内。
文件归并:(每个堆成员的id表示这个成员来自的文件id,其实要保证的是每个文件最多只有一个元素在堆里。也就是去掉一个之后,需要再从其对应文件中再读取一个放到堆里。)
先每个文件读取第一行。每个文件内部按照词频非递减顺序排列.
写入文件有个需要注意的:需要一个缓存,保存当前word1,word2,weight。下一个如果一样则合并,如果不一样则写入old,将新来的当作old。最后再写入缓存old
shuffle.c
外存shuffle,没有什么特别的
glove.c
使用多线程进行求解。why lock-free?因为SGD的性质?不担心丢失部分信息?
gradsq保存的是梯度平方和,用于控制梯度下降速度:adaptive
W用于保存求解的词向量以及basis。每个词向量大小为vector_size, 共vacab_size个词 。
W中的顺序为:word1 词向量,偏置1, word2 词向量, 偏置2,… , word vacab_size词向量, 偏置。 word1 context 词向量, 偏置。。以此类推。
优化目标为公式(8)
直觉上,i的词向量 * j的词向量应该等于两者共同出现的加权频率。 主线程将文件进行划分。每个线程负责一部分。 在每个线程内部:(看注释)