本文主要参考1. 原文写得非常好,墙裂推荐。
决策树是人们日常生活中做决策使用的算法。甚至在没有机器学习之前,人们就开始使用决策树做决策。比如下图这个例子就是人们日常生活中对决策树的使用。
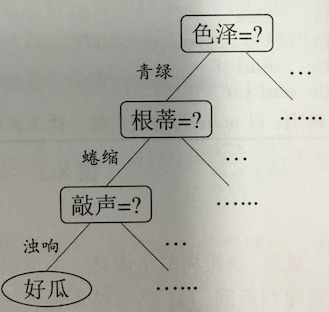
决策树具有训练简单,易解释的特点。在实际中,大量机器学习,数据挖掘任务中都会用到决策树。
基于hmm-gmm的语音识别,合成是建立在基于决策树的状态聚类,绑定上。通常所调的特征,影响的就是状态聚类的结果,进而影响hmm-gmm的训练。

给定属性数据及其对应的标签,如何构造决策树呢?
划分选择
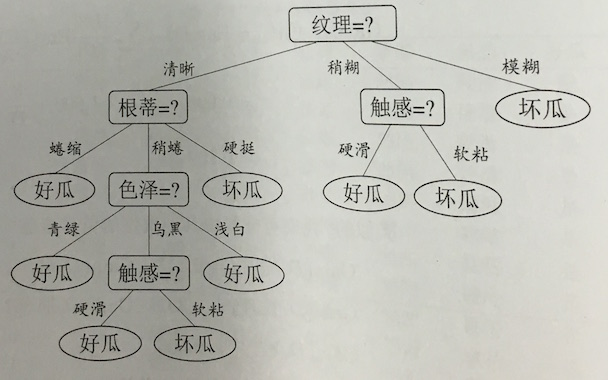
在决策树的学习中,希望更具有划分能力的属性放在更靠近根节点的位置。一般是:每次选择最优划分属性,不断划分节点。我们希望随着划分的进行,分支节点内所包含的样本尽量属于同一个类别。即,节点的纯度越来越高。
那么,现在问题的关键就是如何选择最后划分属性。
决策树可以用于处理分类问题,也可以用于处理回归问题。回归问题可使用均方误差作为划分度量2。本文讨论的主要是分类问题。使用增益,增益率,Gini指数作为度量。

PS:决策树同样可以用于聚类,在hmm语音合成,语音识别中,决策树作为聚类方法,避免由于数据稀疏性,某些三音素模型找不到对应的样本,或者只有很少的样本而造成的问题。
最常用的决策树算法是:ID3,C4.5,CART(Classification and Regression Tree 分类回归树)。 其中分别采用的划分结果度量:增益,增益率,Gini指数。
增益
\[Ent(D)=-\sum_{k=1}^{\lvert y\rvert}p_klog_2p_k\]其中\(D\)表示样本集。\(Ent(D)\)的值越小,则\(D\)的纯度越高。\(Ent(D)\)的最小值为0,最大值为\(log_2\lvert y\rvert\)。
例如,样本总数为17,按照某个属性可以分作两类,个数分别为8,9。则信息熵可以计算为:
\[Ent(D)=-\sum_{k=1}^{\lvert y\rvert}p_klog_2p_k=-(\frac{8}{17}log_2\frac{8}{17}+\frac{9}{17}log_2\frac{9}{17})=0.998\]从上例的计算可以看出,在各类别的样本总数很相近时候,熵的值趋近于\(log_2\lvert y\rvert\)
在对样本进行划分时候,我们希望每个分支的样本纯度越高越好,对应的熵越小越好。定义了信息增益来描述对样本进行划分的收获。信息增益代表样本不纯度的下降。
\[Gain(D,a)=Ent(D)-\sum_{v=1}^{V}\frac{\lvert D^v\rvert}{\lvert D\rvert}Ent(D^v)\]其中\(V\)表示按照\(a\)属性进行划分,可以获得的类别。\(\lvert D^v\rvert\)表示\(v\)类样本的数目。信息增益越大,表示按照该属性划分获得的纯度提升越大。
计算样例:\(D\)样本集按照某个属性\(a\)可以划分为\(D^1,D^2,D^3\)。其中每个样本集中,分别包含\(6,6,5\)个样本。正负样本数分别为\((3,3),(4,2),(1,4)\)。先计算每个分支节点的信息熵: \(Ent(D^1)=-(\frac{3}{6}log_2\frac{3}{6}+\frac{3}{6}log_2\frac{3}{6})=1.000\) \(Ent(D^2)=-(\frac{4}{6}log_2\frac{4}{6}+\frac{2}{6}log_2\frac{2}{6})=0.918\) \(Ent(D^3)=-(\frac{1}{5}log_2\frac{1}{5}+\frac{4}{5}log_2\frac{4}{5})=0.722\)
根据信息增益的计算公式:
\[Gain(D,a)=0.998-(\frac{6}{17}\times1.000+\frac{6}{17}\times0.918+\frac{5}{17}\times0.722)=0.109\]ID3采用增益来作为划分度量。ID3采用多分支结构,每次消耗一个属性。其归纳偏置是,偏好结构简单的决策树。这种结构无法处理连续数值问题。对可取值数目较多的属性有偏好(属性取值多,熵自然就大)。为了减少这种偏好带来的不利影响,C4.5引入增益率。
增益率
\[Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}\]其中
\[IV(a)=-\sum_{v=1}^{\lvert V\rvert}\frac{\lvert D^v\rvert}{\lvert D\rvert}log_2\frac{\lvert D^v\rvert}{\lvert D\rvert}\]\(IV(a)\)称为属性\(a\)的固有值。属性可能的取值数目越多,则该值越大。
增益率准别对可取值数目较少的属性有偏好,C4.5算法也不是直接采用增益率。而是先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的属性。
Gini指数(不纯度)
\[Gini(D)=\sum_{k=1}^{\lvert y\rvert}\sum_{k^{\prime}\ne{k}}p_kp_k^{\prime}\]直观来说,\(Gini(D)\)表示从数据集\(D\)中随机抽取两个样本,其类别标记不一致的概率。Gini值越小,数据集的纯度越高。
剪枝处理
剪枝是决策树学习为了防止过拟合。从直观上来说,如果属性够多,不断划分,很可能使得每个节点的类别都不是纯的。这时就可能因为训练学得“太好了”,以致于把训练集本身的一些特点当做所有数据都具有的一般性质而导致过拟合。可以通过减除一些分支来降低过拟合的风险。
在语音合成的决策树聚类,也有从下到上的合并过程。这样可以避免某些节点因为数据过少而且这部分数据准确性(有可能是噪声)造成的问题。
剪枝方法分为预剪枝和后剪枝。
- 预剪枝:就是在划分节点时候先进行估计,如果划分后会导致泛化性能的下降,则不再划分。
- 后剪枝:先正常划分决策树,待决策树完全长成,再从底向上遍历,如果某个节点替换为叶子节点可以使得泛化性能上升,则替换之。
泛化性能判断通常是通过验证数据集来进行性能评估。
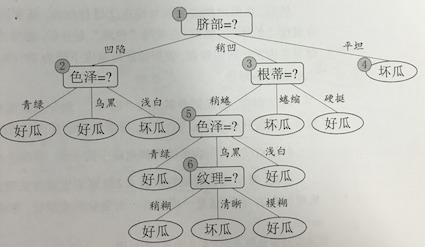
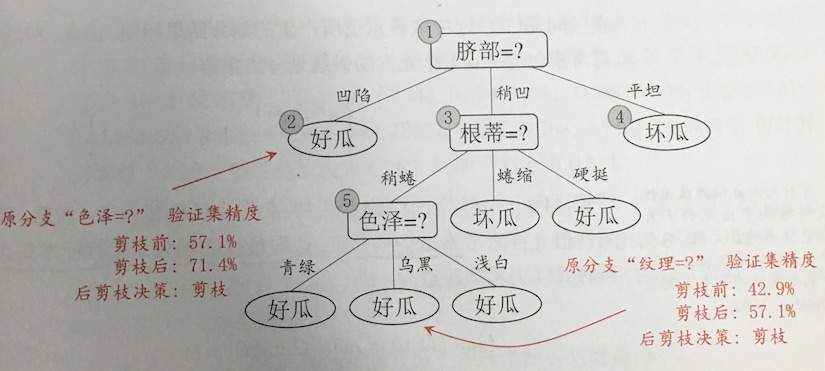
连续值,缺失值
连续值处理
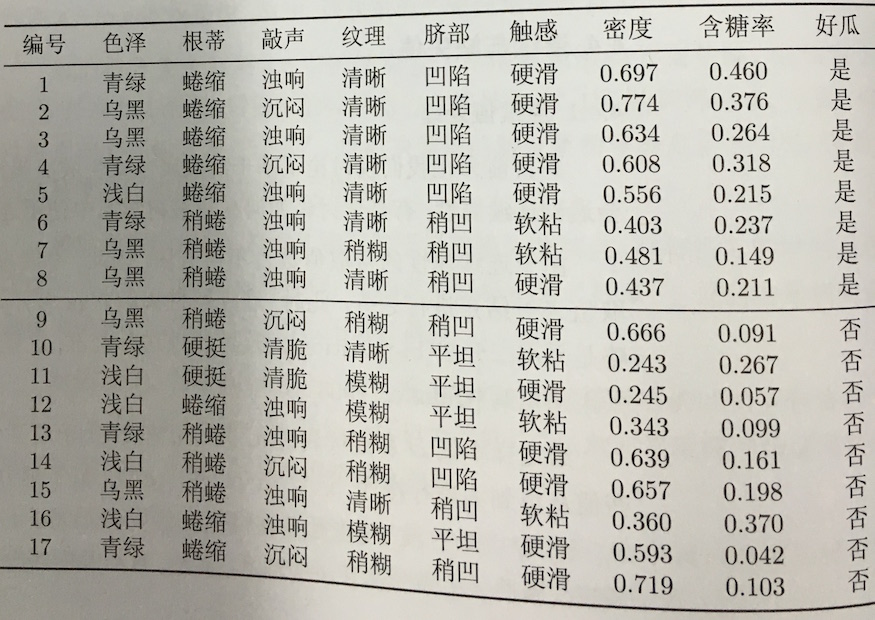
下图在是包含连续值的数据集。密度,含糖率是新的数据。如何评估它们的影响?
通常采用的是二分类法。将该属性值从小到大排序,以任意两个取值的均值作为划分点,并评测其划分性能。选取划分性能最好的划分点进行样本划分。
需要注意的是,连续属性可以重复使用。
缺失值处理
通常的做法有:
-
引入权重概念,缺失值样本按照一定比例分配到各个分类中。
在选择划分属性时,以各个属性的无缺失样本来计算信息增益。挑选信息增益最大的属性作为划分属性。再把缺失样本按比例加入到各个子节点中
-
寻找替换属性。当需要使用该属性划分时,选取与其表现相近的属性