Deep Reinforcement Learning

• 马尔可夫决策过程
• 策略网络(policy network)
• 监督学习
• 策略梯度
• 策略梯度推导

本文探讨使用强化学习的方法，自动玩Pong游戏。

本文主要参考: Deep Reinforcement Learning: Pong from Pixels

Pong游戏如下图所示，两个玩家各控制一个挡板，操作对象是一个小球，在游戏过程中，白球从哪一方穿过，哪一方算失败。

马尔可夫决策过程

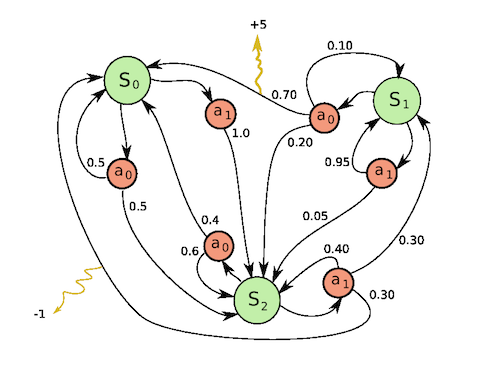
模型中包含环境和agent。agent所处的环境用状态S表示。agent可以针对环境（当前所处的状态）做出action，在action之后，环境的转变体现为状态的转变。在agent的做出action之后，需要对其进行奖励或者惩罚（reward），使其最终能很好地适应环境。

策略网络(policy network)

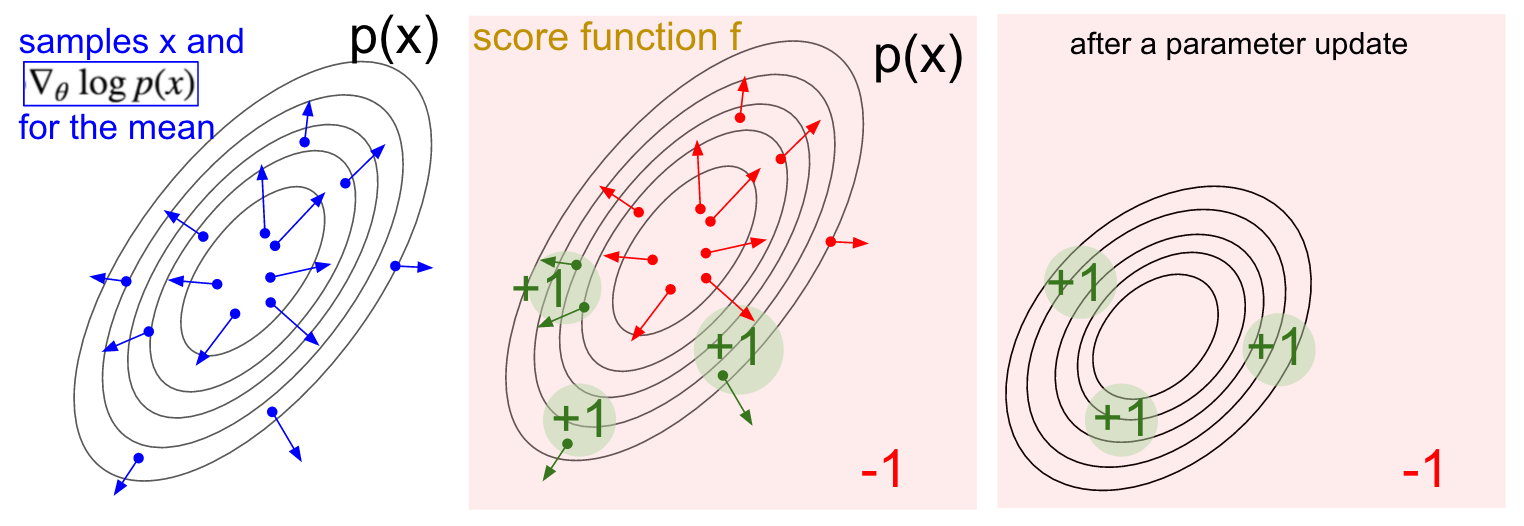
策略网络就是简单的神经网络。用图片的原始像素值作为输入来确定是向上移动还是向下移动（分类问题）。直觉上来说，通过100,800个数字(210*160*3)来做分类需要大量的数据。本文解决两个问题：

1. 在达到最终结果之前，根本不知道前面的步骤应该奖赏还是惩罚。
2. 也有可能前面的多帧的决策都没有问题，由于后面某帧的失误，导致最终失败，在这种情况下怎么处理呢？

左边是由openAI提供的gym运行环境和AI，右边是训练模型的表现。

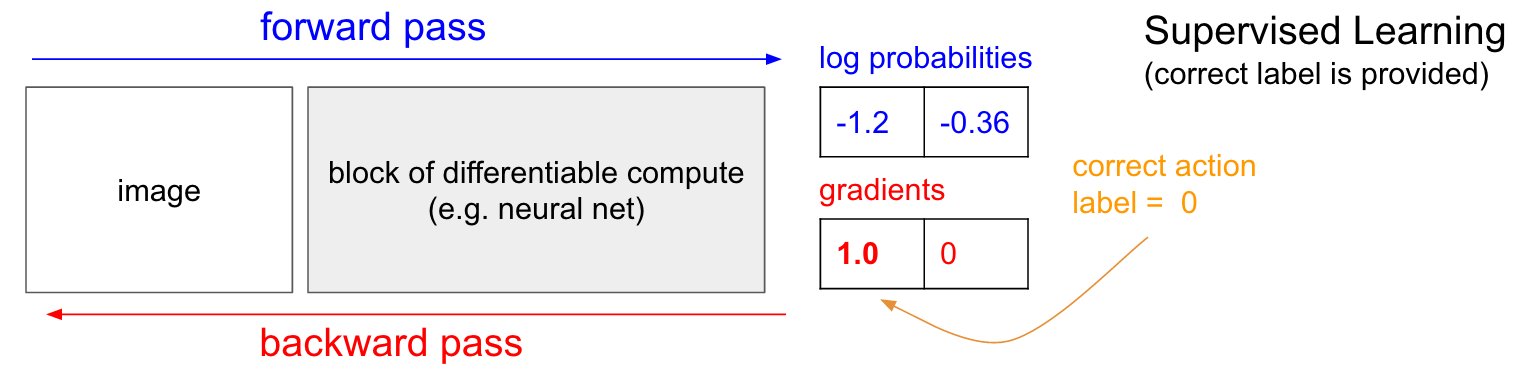
监督学习

在监督学习中，对于每个样本都有一个标签来表示正确的分类结果。先假设在Pong游戏中，我们已经知道每一帧的是应该向下还是向下。我们根据策略网络的预测值，对其做误差方向传播，从而调整模型权重。

策略梯度

上一节讲解了在有标签的情况下，怎么学习策略网络。但是在实际中，我们并没有大量监督数据，解决这个问题的是：策略梯度(Policy Gradients)，深度Q学习 (deep Q learning)。 google deepMind在2013年最初利用deep Q learing学习atari游戏，取得超过人类的结果。但是在之后的研究中，人们发现策略梯度的效果更好（其中包括deep Q learing的作者）。AlphaGo使用的是策略梯度+蒙特卡洛树搜索(Monte Carlo Tree Search).

本文的作者所训练的模型是基于策略梯度。下文主要讲解策略梯度。

再来考虑上文提出的两个问题.

• 问题1中，在游戏决定胜负的时候，可以定义胜利的奖赏是+1，失败的惩罚为-1. 对于中间大量的帧应该使用什么奖赏呢。答案是，在游戏决定胜负之后，根据最终的结果决定对前面的action进行惩罚还是奖励。

  

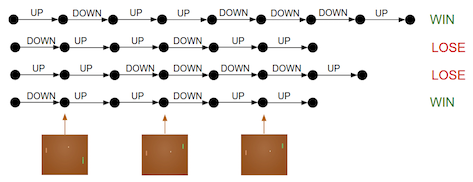
• 问题2：如何处理前面很好，后面由于失误导致的失败呢？答案是: 在不断重复的游戏过程中，前面正确的决策更可能使得最终取得胜利，所以，平均来说，正确决策的所获得的正向更新会高于获得的负向更新。这样，我们的策略最终还是会做出正确的选择。

到目前为止，我们只分胜负，对于胜利+1，对于失败-1。实际上，一般来说，更靠近最终结束的action所造成的影响越大。前面的影响相对较小。应该对此加以区分。用\(r_t\)来标记\(t\)帧所应该获得奖赏。在原来的做法中，\(r_t\)只有获得胜负时候才有，其他的都取为0. 一个做法是：\( R_t = \sum_{k=0}^{\infty} \gamma^t r_{t+1} \). 称为”\(gama\)折扣累积奖赏”。

策略梯度推导