Deep Learning Flappy Bird
Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning[J]. arXiv preprint arXiv:1312.5602, 2013.
mdp
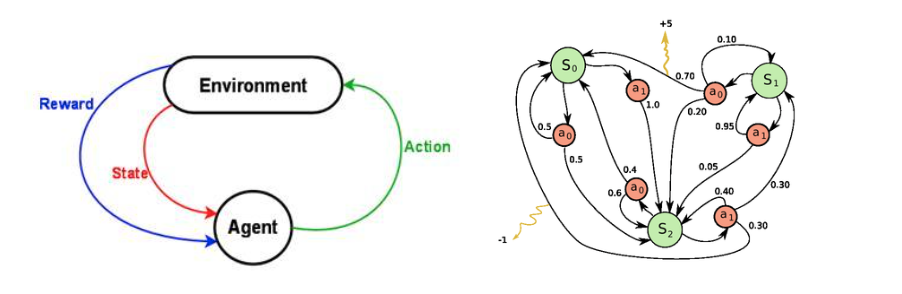
\(s_0,a_0,r_1,s_1,a_1,r_2,…,s_{n-1},a_{n-1},r_n,s_n\)
针对当前状态\(s\)做出行为\(a\),获得奖赏值\(r\),直到最终达到终止状态\(n\)
折扣奖赏
在强化学习的应用场景中,通常存在直到最终状态之前不知道决策好坏的情况,称为奖赏延迟。对于这种情况,上次我们在分析pong的时候使用的是折扣奖赏。就是从最后结果中反推前面每一帧应该获得的奖赏值。
\( R_t = \sum_{k=0}^{\infty} \gamma^t r_{t+1} \)
强化学习要做的就是通过某种方式得知当前状态下做出哪种行为将获得更大的奖赏值。训练方法有:Q学习,策略梯度
Q学习
Q学习中定义Q函数:\(Q(s,a)\)表示在状态\(s\)采取\(a\)行为所能获得的最大奖赏值。
\(Q(s,a)=max(R_{t+1})\)
可以理解Q函数为:在s状态下采取了a行为后,游戏结束所能获得的最高得分。之所以叫做Q函数Q-function,因为他代表了在某种状态下采取某种行为的质量quality。这是一种值函数近似。
在训练时候我们采集\(<s,a,r,s’>\)序列,那么,Q函数可表示为:
\(Q(s,a)=r+{\gamma}max_{a'}Q(s',a')\)
称为Bellman equation
在训练中,最重要的技巧是:experience replay。在训练时,收集大量这种四元组序列,再随机采样进行训练。这样避免了大量相似的序列,避免局部最优,而且这样与监督学习更加相似,容易调试。
在Q学习中,通常使用Bellman equation来近似Q函数。简单的Q学习(表格值函数)实现如下:

deep Q network
deep Q network其实就是使用神经网络来估计Q函数。神经网络的输入时图片,输出是采取各个行为所能获得的Q函数。
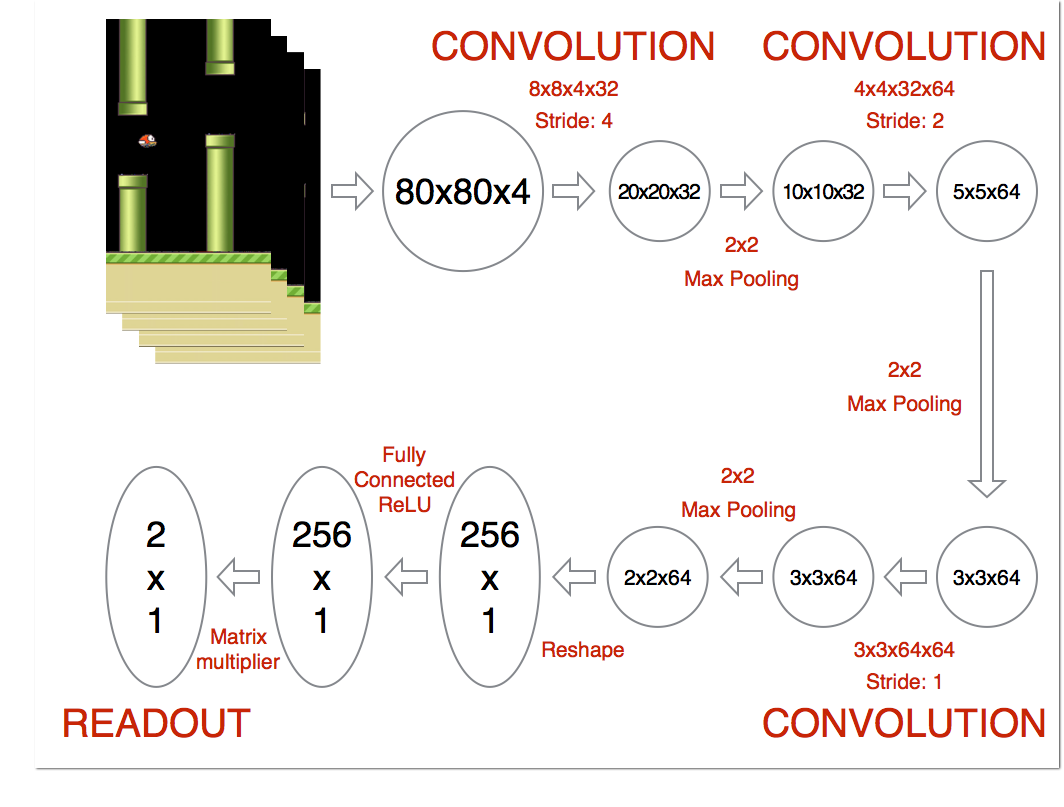
在flappy bird的例子中,输入时连续四帧图片。输出READOUT用来表示在这情况下,是否“跳”所能获得的奖赏。
在学习的时候会对图片做个预处理,就是简单的阈值操作。
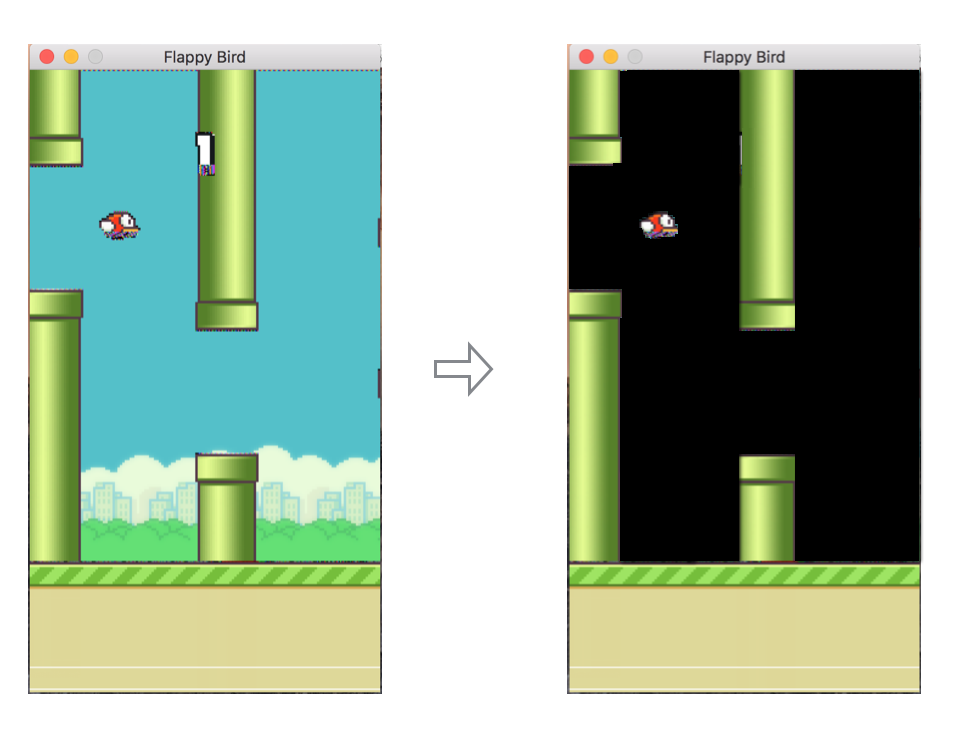
那么我们要学习的目标就是:
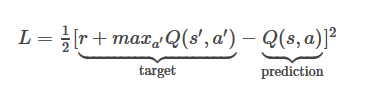
这里\(Q(s’,a’)\)也是神经网络的预测值。我们要优化的目标是当前神经网络对于s状态的估计值于通过后向传递获得的估计值的残差。那么,训练时候获得整个运动序列的作用仅仅只是想要知道\(s\)状态所能转移的下一个状态\(s’\),也就是当前图片显示的flappy bird在按了一下跳或者不跳后,图片会变成什么样子。
那么这里就涉及到选择策略:探索(exploration)和利用(exploitation)。
探索和利用
在s状态下,我们估计出选择跳还是不跳所能获得的奖赏值。跳和不跳会使环境到完全不同的状态\(s’\). 这个策略直接决定了我们下面能获得的图片是什么。选择策略主要包括以下两种:
利用:选择当前估计奖赏值最大的行为。这种方法是根据历史经验来选取最优。缺点是可能陷入局部最优。 探索:按照一定概率选择不同的行为。这种方法不会陷入局部最优,缺点是很难收敛。
以上两种方法各有优劣,称为探索-利用窘境。一般需要取折中方案。有一种方法是\(epsilon\)贪心探索(ε-greedy exploration)。在每次选择时候,按照\(epsilon\)的概率进行随机选择,\(1-epsilon\)选择奖赏最大的行为。在实际的操作中,\(epsilon\)可能随着时间慢慢减小。
算法流程

深度Q学习和策略梯度
- 深度Q学习: 用cnn来估计Q函数。要学习的目标是:当前状态的估计Q函数和下一个状态反向获得的奖赏的误差最小。
- 策略梯度:奖赏值是从结束状态往回传递。要学习的目标是:
当前估计的行为的概率和实际采取行为的误差乘以反向奖赏值.