加权有限状态转换器

• 例子
  • 语言模型
  • 发音字典
  • 合并
  • 确定化
  • 最小化
  • 删除辅助符号
  • 总结
• 基本概念
  • weighted acceptor
  • weighted transducers
  • 半环（semiring）
• 操作
  • Composition
  • Determinization
    • Determinization automation
    • Determinization transducer
  • Minimization
    • weight push:
    • true minimization
  • \(\epsilon\) remove
  • Fractoring
• Speech Recognition Transducers
  • grammar
  • lexicon
  • context
  • hmm

加权有限状态转化器算法是现在语音识别解码器的有效算法。是语音识别的核心。语音识别结果的好坏一定程度上取决于解码器的好坏。kaldi基于openFst构造解码器。

例子

一个完整的语音识别流程如下图：

语言模型

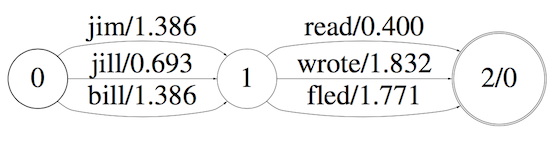
这只是一个简单的例子，只接受两个词的训练，并且这两个词是上面所示的这个组合。更完整一点的例子是：

发音字典

在发音字典中，接收的是音素(在汉语中可以简单理解为，音素就是拼音)，输出的是词。

合并

现在假设我们的识别系统最小的单位就到音素级别，那么，在识别的时候，对于每个发音单元，我们会获得其属于每个音素的概率，那么到底应该怎么使得整个输出符合字典，同时符合人类说话的习惯（语言模型）。

一个最直接的想法是合并以上两个转换器。合并观测概率和语言模型的转移概率。

确定化

从上图发现我们在收到jh的时候并知道应该走哪条路径，这样会使得搜索代价增大。确定话要做的事情就是将相同的路径合并。如下图的jh所示。在合并之后需要做的事情有：

• 延迟输出： 因为是多个路径的合并，所以暂时无法确定输出
• 记录权重： 因为多个路径的权重可能并不相同，所以在合并的公共路径上记录最小权重。而将部分剩余权重记录，在后面部分加入。

图中红色标记1表示在合并之后的剩余权重。

标记2表示，在状态9只要输入f就可以确定输出是fled了。在这里为何不怕前一个识别结果是f，后一个识别结果不是l的情况？这是因为由于grammar的关系，在composition的时候，该位置不输出l的结点都被干掉了。在极端的情况下，如果grammar只有一个词，那么无论输入的语音是什么，结果都会是这个词。

标记3处表示，在当前位置无法获得确切输出，则输出延迟。

最小化

最小化要做的事情就是我们发现上面网络可能有些冗余部分，这部分会导致存储空间，计算时间的增加。所以，通常会加上最小化操作。

最小化操作的步骤通常包括：权重推送，最小化。具体参见后文。

最小化的过程中先进行了权重推送。

图中标记部分分别推送了0.693，0.4的权重。所以在最终节点处增加1.093权重

删除辅助符号

后文细讲。

总结

从上文可以看出，在wfst进行语言识别的过程中，需要准备的数据有，语言模型，发音字典。主要涉及的操作是：合并(Composition)，确定化(Determinization)，最小化(Minimization).

下面我们先介绍一下基本概念。再分别介绍这几个操作的具体算法。最后介绍在语音识别中具体应该怎么构造这些组件。

基本概念

weighted acceptor

以加粗的圆圈为起点，以双圆圈为终点。也称为weighted finite automata。加权有限自动机。边的格式为：输入符号/权重。

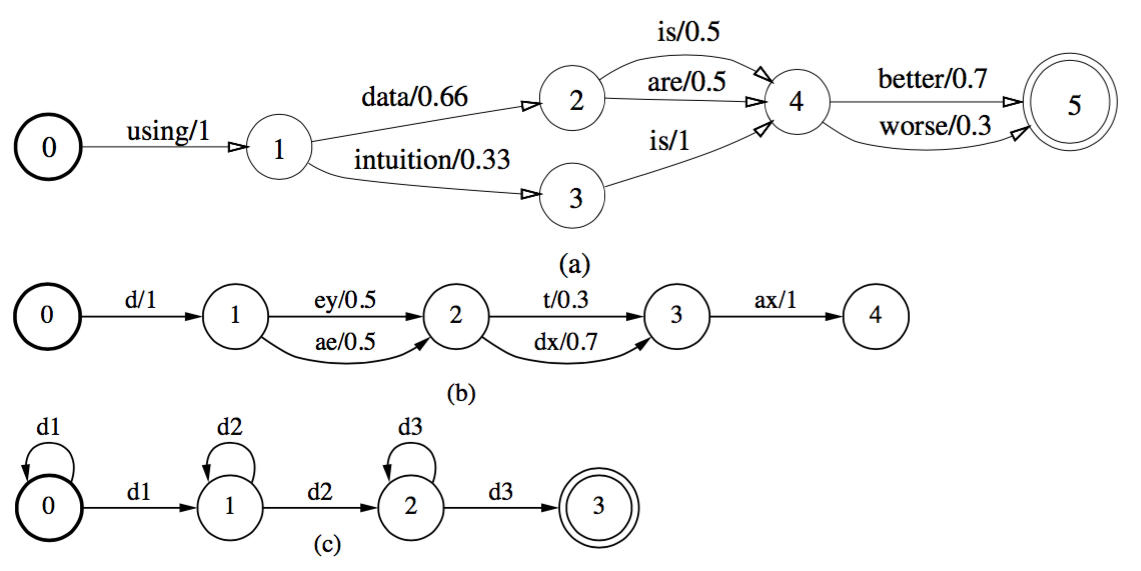
weighted transducers

加权有限转换器。加权有限转换器的结点表示状态，边的格式为：输入符号：输出符号/权重。

在有些图中会碰到\(\epsilon\). 这个符号在输入时表示不消耗任何输入，在输出位置表示不产生任何输出。

加权有限转化器相对于加权有限自动机的优点在于：加权有限转换器在输出位置进行输出，这样可以使得多个符号一起输出的时候不会损失可识别性。

甲醛有限自动机的这种特性经常被用来表示不同级别的表示之间的关系。更准确的说，加权有限转化器可以表示出，在序列上的所有输入组成的字符串和所有输出组成字符串之间的关系。

不同级别之间的转换器使用Composition来进行合并。使用Determinization来删除无用的边。使用Minimization来进行最小化，从而优化计算和存储效率。

半环（semiring）

本文最常用的半环是tropical半环。可以简单理解为：在路径上求和并取最小。

以下是详细一点的介绍：

在转化器上的计算可以看做在半环的操作。（？）

半环的种类有：

计算实例：

这个例子中分别展示了probability半环, tropical半环的计算例子。

在实际中，更常见的是log半环和tropical半环。如果，边上的权重是概率的负log值，则，tropical半环是log半环的verbi approximation.

操作

Composition

Composition用来合并不同级别的转换器。用\(T=T_1\circ T_2\)表示这种操作。

比如下面这个图，体现了Composition的基本操作。图a，b分别表示进行合并的两个图。其下方表示合并结果。

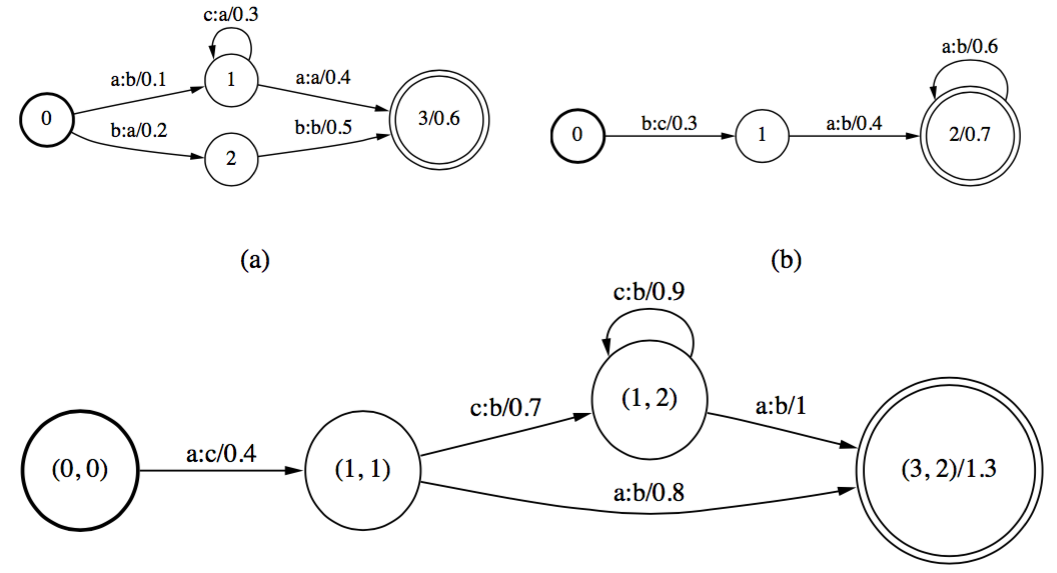
从这个图中体现了几个原则：

• 起始状态应该是T1，T2的起始状态
• 结束状态是T1，T2的结束状态
• 如果\(q_1\)到\(r_1\)的边\(t_1\)的输出等于\(q_2\)到\(r_2\)的边\(t_2\)的输入，那么\((q_1,q_2)\)和\((r_1,r_2)\)应该有一条边，如果是tripical半环，则该边权重是以上两边权重之和

以下是Composition的例子，图中详细标注了计算方法。

注意：当T1的输出包含\(\epsilon\)， T2的输入包含\(\epsilon\)的时候，需要额外处理。

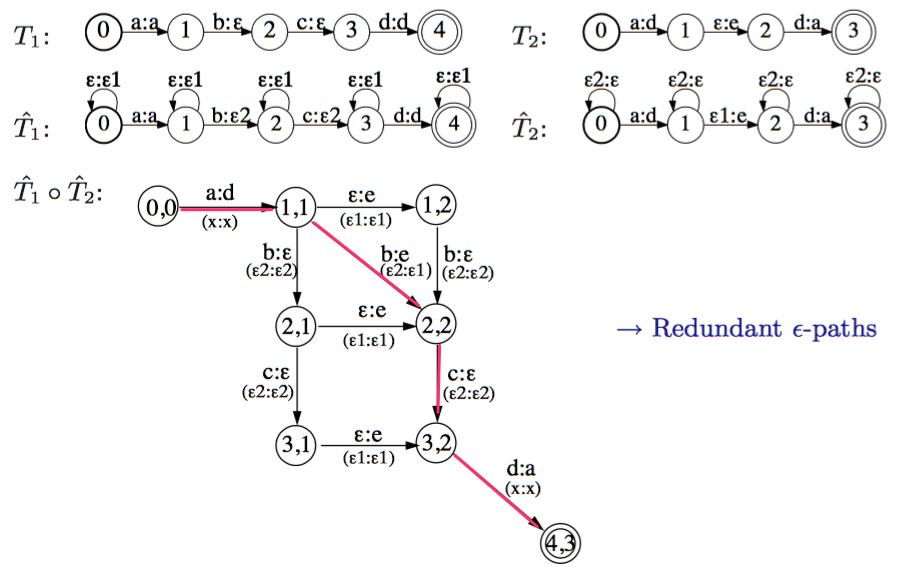
如上图所示，T1，T2的输出，输入分别包含\(\epsilon\)，会导致产生大量多余的边，使得最终结果不正确。常用的解决方法是先将T1中的\(\epsilon\)写成\(\epsilon2\)，将T2中的\(\epsilon\)写成\(\epsilon2\). 并将转化后的结果记为：\(\tilde{T}_1\),\(\tilde{T}_1\). 如上图所示。

并且为了避免重复无用的路径，加上一个过滤器F。这个过滤器也可用transducer表示如下图左图。希望用\(T=T_1\circ F \circ T_2\)来表示\(T=T_1\circ T_2\)

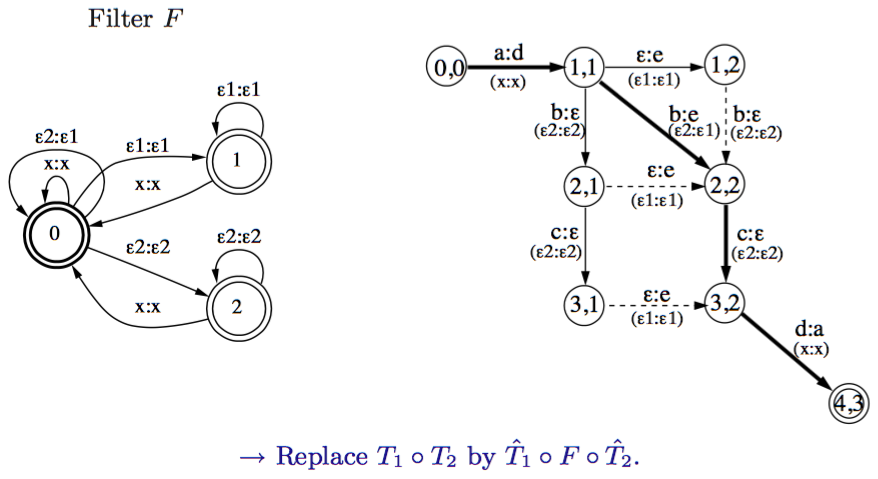
上图右图括号中(x,x)表示F中的转移边。加以过滤之后，会将上图中虚线边去除。在F中，并没有\(\epsilon2:\epsilon2\)到\(\epsilon1:\epsilon1\) ，所以在图中状态2,1到状态2,2,以及状态3,1到3,2的边将被去除。

那么，现在问题转化为：F中的转移状态应该如何确定呢？其设计原则应该是避免\(\epsilon2:\epsilon2\)到\(\epsilon1:\epsilon1\)以及\(\epsilon1:\epsilon1\)到\(\epsilon2:\epsilon2\)成为相邻的边.

Determinization

Determinization: 所有状态在接受某个输入后只有一条输出边，而且不包含\(epsilon\)

Determinization的根本前提：两个自动机或者转换器是否相等，不需要每条边，每个权重都相等。只需要对于任何一个输入序列，其输出及权重相同，而不用在意权重的分布是否相同。

一般使用\(\otimes\)来计算分支内的权重。使用\(\oplus\)来处理分支间最终输出的权重。根据\((\otimes, \oplus)\)的不同，分为：tropical半环(tropical semiring)，log半环(log semiring)。

Determinization automation

自动机确定话状态内部信息表示：{原始状态号,剩余权重}

上图中，从(0,0)到(1,0)(2,1)的边a/1上消耗权重1，原图状态1，状态2剩余权重分别是0和1，所以用(1,0)(2,1)表示。 在输出到下一个状态时候，将剩余权重加上。比如原图中d/6,这里变成d/7

Determinization transducer

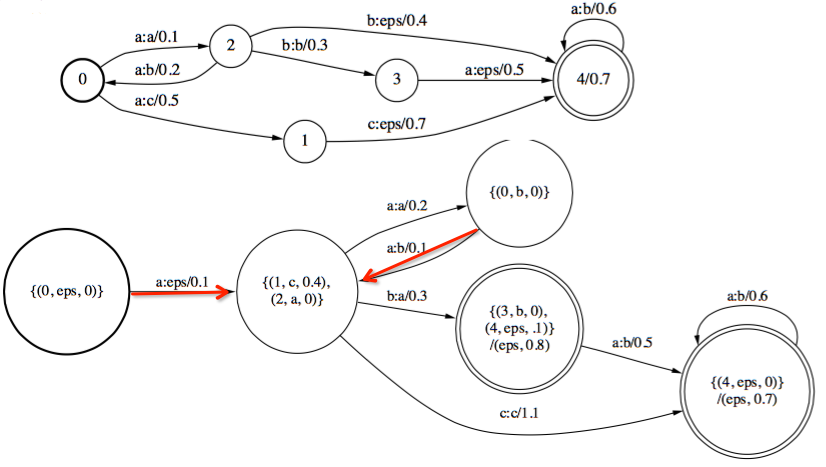
转换器确定化状态内部信息表示：{原始状态号，待输出，剩余权重}

图中红线部分其实表示相同的转移边。

确定化大致流程：碰到相同的输入，则合并之，取最小权重。剩余权重后推，输出后推。这点后文lexicon可以更加清楚其作用。

Minimization

最小化的目的是减少原图中的状态数，以及转移边数。从而减少存储空间和计算时间。

最小化一般是消除相同结点。常用算法与DFA的最小化算法类似(?).

但是有时候并没有相同的结点，比如下图a部分。在这种情况下，一般先进行权重推送(weight pushing)，然后再进行最小化。

下面先介绍权重推送。

weight push:

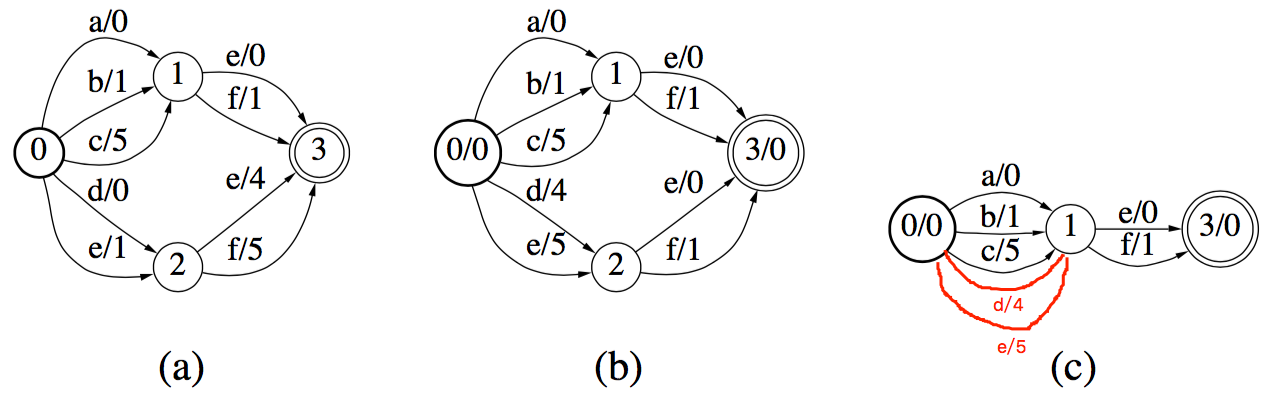
前面说过，转换器跟权重的分布没有关系，只和最终权重的大小有关。所以可以将权重前推，以利于最小化。可以使用网络的方法进行权重推送。但是为了效率，一般采用单源最短路径算法来代替。权重推送是讲权重往前推。等价于，使得每个结点到结束结点的权重最小化。在上图a中，状态2到结束结点3的权重最小化到0，那么e/4,f/5的最小权重是4.将这部分权重前推之后，如上图b所示，e，f的权重均减少4，前面结点的权重加4. 如果有更多结点，则一次前推。从最终的结果看，除了结束结点之后，每个结点到结束结点的最小路径为0.

true minimization

通过权重推送之后，发现状态1，状态2是相同的结点，则可以将其进行合并。如上图c所示。原文有误，红色路径是我加上的

更完整的例子：

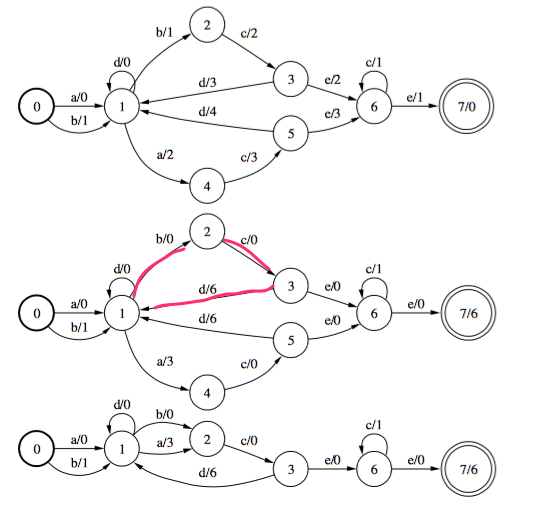
上图分别体现了权重推送，最小化。我们先来考察一下上图权重推送之后与原图的等价性。等价性体现在每一个路径不管权重分布如何，权重总和应该是相同的。

上图中，红线部分状态1，2，3所构成的环，不管其权重分布，权重总和是一致的。同理，状态1，4，5构成的环权重和也是一致的。

再来考察一下路径1，2，3，4，6的权重和是否相同。在这里，因为权重推送的关系，大部分的路径的权值都为0。图中在结束结点7上添加上被推送损失的权重6.

ps: 在kaldi中并没有pushing操作。

\(\epsilon\) remove

对于部分输入输出都包含\(\epsilon\)的，需要先将该边去除。详见下图。

Fractoring

该步骤可以大大减小模型大小。

为了表示变长hmm，将每n长度映射到n状态hmm。

其中，\(H^\prime\)是映射关系，\(F\)用来表示实际包含哪些hmm转台。应该类似于pca的做法？

Speech Recognition Transducers

grammar

正常的grammar如上图所示。语言模型需要解决的问题是：给定当前字\(w_1\)，下一个字是\(w_2\)的概率是多少。

使用负log概率表示为：\(-log(p(w_2)\mid p(w_1))\)

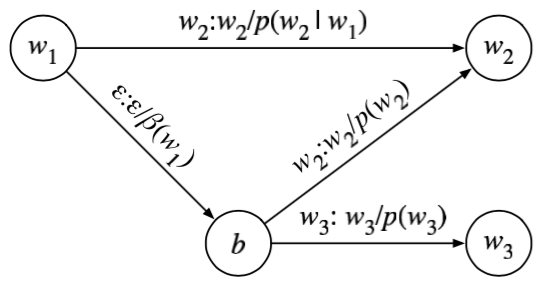
对于部分在bigram中没有出现的词组\(w_1,w_3\)。 其解决方案是增加一个回溯结点b。\(w_1\)到\(w_3\)的概率表示为回溯概率\(\beta(w_1)\)和unigram概率\(p(w_3)\)的乘积。

对于\(w_1\)到\(w_2\)这种有直连边存在的词，不需要刻意禁止回溯边的\(w_1,b,w_2\),因为正常情况下，前者的概率远大于后者。

表达式：

lexicon

发音字典。

为了处理同音字，需要加入消歧符号：#0，#1等。如下所示：

r eh d #0 read
r eh d #1 red

发音字典如下图所示，每个字构成环。称为：Kleene closure. 表示每个字在接受完整输入音素之后，输出对应的字之后，开始接受下一个字的输入。

为了尽量节省计算时间，在第一个输入的时候就输出对应的字。后面的输入不再进行输出，仅作为消耗输入的作用。这里可能有人会问，如果第一个输入相同怎么办，到底应该输出哪个？参考前面的介绍determization部分，如果相同输入，则输出推迟。

表达式：

context

为了方便，我们用context independent phones 到 context dependent phones的映射来说明问题。在实际应用的时候，实际上需要的是context dependent phones 到 context independent phones的映射。只需要将其输入输出倒置即可。

context dependent phones格式为：phone/leftcontext_rightcontext. phone/leftcontext_rightcontext作为一个输出整体而存在。k ae t的模型如下图所示：

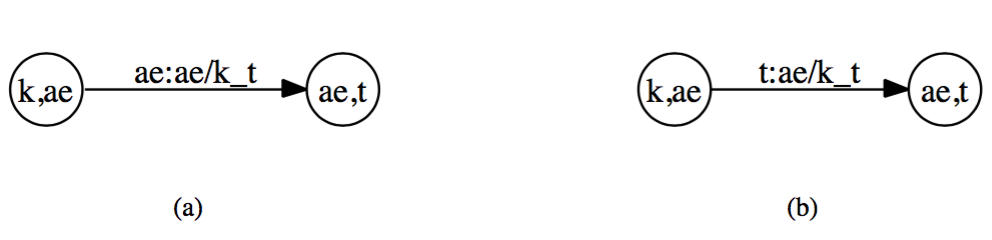
上图a表示输入中间音素的时候，输出对应的三音素模型，右边图b表示，在输入最后一个音素的时候，才输出对应的三音素模型。 从下图可以发现，中间音素输出是非确定的，最后一个音素输出是确定的。

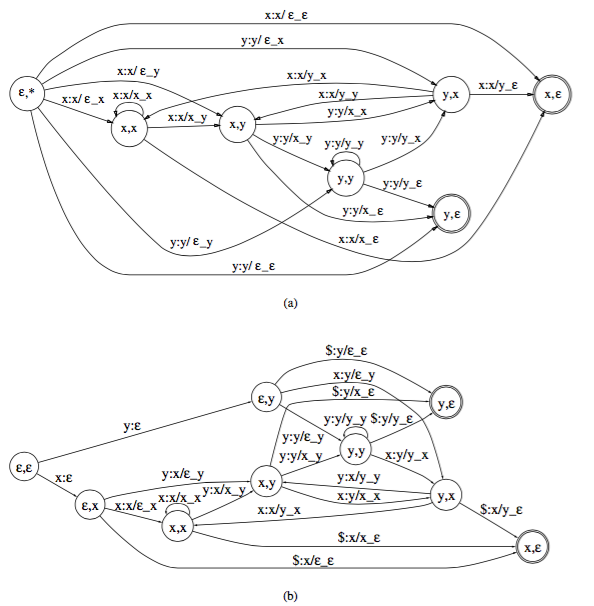
简单的可以理解为：在中间音素输出，可能存在前面两个音素完全一样的情况，而在最后一个音素输出，则不会出现重复。所以前者是可确定的，后者非可确定。

表达式：

hmm

\(H\circ C\circ L\circ G\)

Mohri M, Pereira F, Riley M. Speech recognition with weighted finite-state transducers[M]//Springer Handbook of Speech Processing. Springer Berlin Heidelberg, 2008: 559-584.

OpenFst: An Open-Source, Weighted Finite-State Transducer Library and its Applications to Speech and Language