本文介绍thulac分词,词性标注所使用平均感知机算法。
可以带着一下问题进行阅读:
- 什么是平均感知机?
- 怎么将特征数字化?ngram特征?
- 多分类问题?
- 模型保存的是什么?怎么压缩?
感知机
设输入$n$维输入的单个感知机(如下图所以)。$a_1$至$a_n$为$n$维输入向量的各个分量。$w_1$至$w_n$为各个输入分量连接到感知机的权重。$b$为偏置,$f(.)$为激活函数($f$一般为符号函数)。$t$为标量输出。
\[t=f(\sum_{i=1}^{n}w_ix_i+b)=f(w^Tx)\]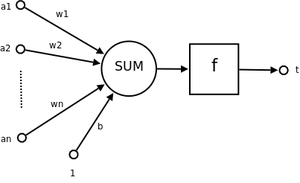
权重迭代:
对于每个$D_n=[(x_1,y_1),(x_2,y_2),(x_3,y_3),…,(x_m,y_m)]$中的每个$(x,y)$对,进行权重更新:
\[w(j)=w(j)+\alpha(y-f(x))x(j)\]平均感知机
模型与感知机相似。只是在训练每个样本的时候,记录其权重,并且更新其当前权重。等到所有迭代完毕之后,计算整个过程的平均权重。这样做的好处是更加鲁棒。

基于平均感知机的分词和词性标注
特征构造
在自然语言处理任务中,一般需要考虑上下文特征。比如说,上一个字是什么,下一个字是什么,上一个字词性(注意,没有下一个词性)。应该包含了ngram特征的构造?
def _get_features(self, i, word, context, prev, prev2):
def add(name, *args):
features[' '.join((name,) + tuple(args))] += 1
#features[' '.join((name,) + tuple(args))] = 1 #个人认为value直接设置为1即可
i += len(self.START)
features = defaultdict(int)
# It's useful to have a constant feature, which acts sort of like a prior
add('bias')
add('i suffix', word[-3:])
add('i pref1', word[0])
add('i-1 tag', prev)
add('i-2 tag', prev2)
add('i tag+i-2 tag', prev, prev2)
add('i word', context[i])
add('i-1 tag+i word', prev, context[i])
add('i-1 word', context[i - 1])
add('i-1 suffix', context[i - 1][-3:])
add('i-2 word', context[i - 2])
add('i+1 word', context[i + 1])
add('i+1 suffix', context[i + 1][-3:])
add('i+2 word', context[i + 2])
return features
怎么将特征数字化?从上面的特征构造可以发现,出现次数越多的特征,其特征值越高(该feat的value较高,weight需要训练)。
在词性标注或者分词任务中,需要分的类别往往不只两类。如果考虑整个句子的分类效果,则需要使用viterbi等解码算法。但也有只考虑当前状态,输出当前样本的所属最大概率的类别。
不采用解码算法
对于词性标注任务,可以不参照上下文的标注结果。直接使用贪心算法即可。
多分类问题?对于这种多类别任务,可以使用多分类器。在预测的时候,哪个分类器概率高,就采用该分类器所属的类别。个人认为这里value都设置为1即可。
def predict(self, features):
'''Dot-product the features and current weights and return the best label.'''
scores = defaultdict(float)
for feat, value in features.items():
if feat not in self.weights or value == 0:
continue #某些特征没有权重不造成出错
weights = self.weights[feat]
for label, weight in weights.items():
scores[label] += value * weight #实际上value都设置为1即可?
# Do a secondary alphabetic sort, for stability
return max(self.classes, key=lambda label: (scores[label], label))
注意上面某些特征的没有权重不会影响结果。所以可以考虑把删除很少出现的特征,以减小模型大小。
在训练的时候,对于每个样本都有一个真实标签truth并且基于当前模型给出一个预测标签guess。如果这两个标签相同,则说明当前权重暂时不需要调整。如果不同,则需要对于给出正确标签的特征的权重进行加权,对于给出错误标签的权重进行降权。
def update(self, truth, guess, features):
'''Update the feature weights.'''
def upd_feat(c, f, w, v):
param = (f, c)
self._totals[param] += (self.i - self._tstamps[param]) * w
self._tstamps[param] = self.i
self.weights[f][c] = w + v
self.i += 1
if truth == guess:
return None
for f in features:
weights = self.weights.setdefault(f, {})
upd_feat(truth, f, weights.get(truth, 0.0), 1.0)
upd_feat(guess, f, weights.get(guess, 0.0), -1.0)
return None
注意: 因为这个权重的键值是<(feat, label), weight>。key是非常稀疏的。在使用平均感知机进行权重累计(weight累积的是某个特征权重的真实值。而不是权重变化量)的时候,可能一个特征几百年不出现一次。但是最终又想要除以总的样本数。。为了解决数目不对的矛盾,对每个特征上次出现时间进行记录(在上面代码中表现为self._tstamps, 意即timestamp)。在下次出现的时候,往这两个时间点之间的所有权重值都填上上次权重值。这样使得总的权重数目是对的,才能保证平均的准确性。
使用解码算法
对于分词任务来说,B,M,E,S不是任意组合都是合法的。所以考虑转移概率。代码参考这里。
注意:
- 预测时候需要使用viterbi解码
- 需要添加label到label的转移权重学习