关于反卷积deconvolution这个说法是不准确的, 正确的术语应该是transposed convolution, 两者说的是一个东西,但是还是有一些框架在使用. 本文的主要参考资料是theano_doc, 关于cnn的中文推导以及相关索引资料可以参考这里. 还有一些尚未解决的疑问.待研究代码后解决.
cnn border mode
theano中,可以直接指定border_mode=(p1, p2), 分别的pad值, 也可以直接使用一下三种模式: valid, half, full. 使用方式类似于: border_mode='full'
简单的几种模式:
- valid: 不加pad
- half: 保证输出大小和输入大小相等
- full: pad的大小等于卷积核大小-1, 这样可以使得任何一个像素都被充分利用.
transposed convolution
接下来我们来谈谈deconvolution是怎么实现的,以及怎么反向梯度传导. 下图是正向过程.

每个节点都与卷积有千丝万缕的关系,似乎很难理清楚. 将其转化为以下稀疏矩阵就很明白了:

这个矩阵记成$C$: 4 * 16
将原始图片flatten成16*1的向量, 那么这个卷积过程可以表示为:
\[(4 * 16) * (16 * 1) = (4 * 1)\]即:
\[Cx=y\]把这个输出reshape成(2*2)之后就是所要得到的featuremap.
想要把这个过程逆回去,只要:
\[C^TCx=C^Ty\]大小为:
\[(16*4)*(4*16)*(16*1)=(16*4)*(4*1)\]至于$C^TC\neq I$, 无法进行约简的问题,其实不要在意.因为我们实际上不是想从y求得x,而是想要把y的梯度传递回去。可能也正是这个原因所以叫反卷积并不合适。todo: 既然无法逆转,那么cnn的可视化是怎么做的呢?
从梯度方向传播的角度来说$\Delta x=\frac{dy}{dx} \Delta y$
所以,我们实际上想知道的是,哪些y由同一个x产生的影响.比如说上图,我们知道第一个x只影响了第一个y,以此类推.
根据线性方程的求导,
\[\frac{dy}{dx}=C^T\]所以:
\[\Delta x=C^T\Delta y\]所以,transposed convolution指的是以上式子的transposed.而如果是大图,可能需要对卷积核进行180度翻转?
todo: 参考这个代码
翻转
以下反卷积图示种肯定跟$C^T$不是对应的,两者的维度都不一致.要用下面的矩阵进行卷积的话,稀疏矩阵的维度必须是:
\[(16*36)*(36*1)=(16*1)\]直接将$C^T$求逆显然无法做到.
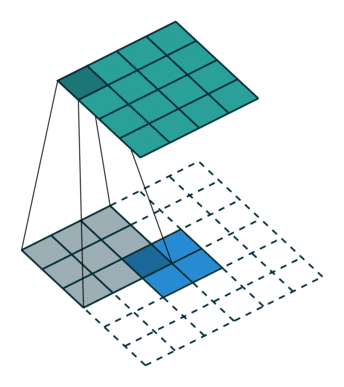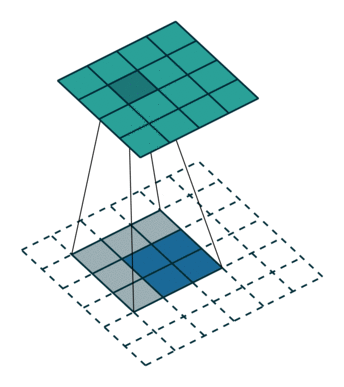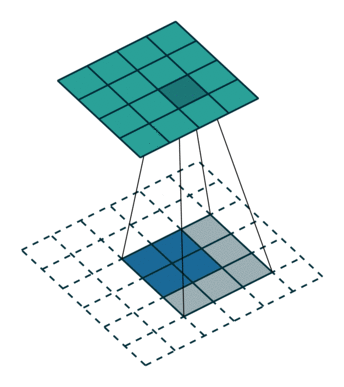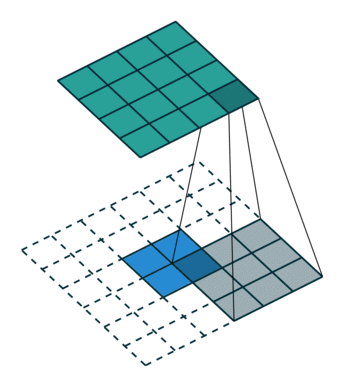
上图卷积过程进行展开之后与$\Delta x=C^T\Delta y$式子一致???应该是要将卷积核180度翻转(即先上下翻转再左右翻转)??
以下例子来自博客
输出加pad:
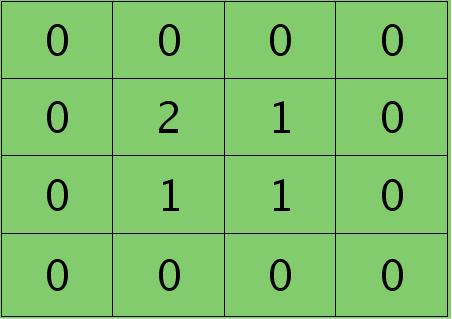
卷积核:

求梯度:
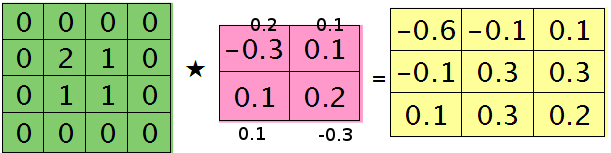
那么这样问题3这样解的依据是什么呢?其实很简单,本质上还是bp算法,即第l层的误差敏感值等于第l+1层的误差敏感值乘以两者之间的权值,只不过这里由于是用了卷积,且是有重叠的,l层中某个点会对l+1层中的多个点有影响。比如说最终的结果矩阵中最中间那个0.3是怎么来的呢?在用2×2的核对3×3的输入矩阵进行卷积时,一共进行了4次移动,而3×3矩阵最中间那个值在4次移动中均对输出结果有影响,且4次的影响分别在右下角、左下角、右上角、左上角。所以它的值为2×0.2+1×0.1+1×0.1-1×0.3=0.3, 建议大家用笔去算一下,那样就可以明白为什么这里可以采用带’full’类型的conv2()实现。
todo: 原文有问题,需要将卷积核的数字进行翻转??
上采样
那么问题来了,如果反卷积的stride 大于1呢?也就是如果需要升采样呢?
参考知乎上这个回答
上采样就是把[W,H]大小的feature map F_{W,H}扩大为[nW,nH]尺寸大小的\hat{F}_{nW,nH},其中n为上采样倍数。那么可以很容易的想到我们可以在扩大的feature map \hat{F}上每隔n个位置填补原F中对应位置的值。但是剩余的那些位置怎么办呢?deconv操作是把剩余位置填0,然后这个大feature map过一个conv。扩大+填0+conv = deconv操作。插值上采样类似,扩大+插值=插值上采样操作。