本文从非参数方法起源开始谈起,再到核方法对于线性回归问题的表示。再讲解核方法中,高斯过程以及其具体应用例子。最后推导svm。
先以prml中文版页码为准。
1. 参数方法与无参数方法
机器学习算法可以分为参数方法和无参数方法。
- 参数方法就是概率分布都有具体的函数形式,通过少数参数确定,在训练之后与训练数据没有关系。称为: 概率密度建模的参数化( parametric )方法.
- 无参数算法不是说没有参数。而是没有固定参数数量。这类算法需要记录训练数据,根据训练数据的不同,模型大小不一样。这种方法对概率分布的形式进行了很少的假设
常用的无参数算法有: 近邻方法,核方法。
从$k$近邻方法为例来理解无参数方法。$k$近邻在训练阶段保存训练数据,在预测阶段,找到其最靠近的$k$个数据点,由这些点投票获得当前点的类别。
首先让我们讨论密度估计的直方图方法。我们集中于一元连续变量 x 的情形。标准的直方图简单地把 x 划分成不同的宽度为$\Delta_i$的箱子,然后对落在第 i 个箱子中的 x 的观测数量$n_i$进行计数。为了把这种计数转换成归一化的概率 密度,我们简单地把观测数量除以观测的总数 N ,再除以箱子的宽度$\Delta_i$,得到每个箱子的概率的值:
\[p_i = \frac{n_i}{N\Delta_i}\]如下图所示:
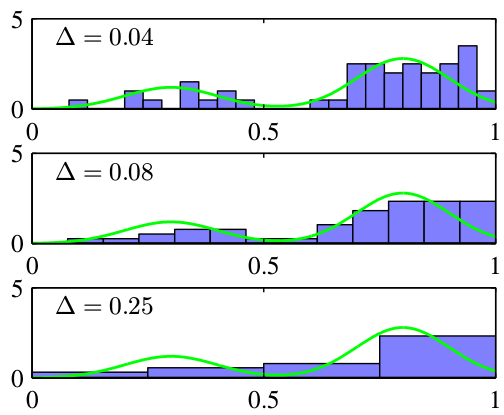
概率密度估计的直方图方法确实告诉了我们两个重要的事情。第一,为了估计在某个特定位置的概率密度,我们应该考虑位于那个点的某个邻域内的数据点. 第二,为了获得好的结果,平滑参数的值既不能太大也不能太小。
把区域R取为以$x$为中心的超小立方体,其体积为$V$, 总数据点数为$N$, 落在这个立方体中的数据点的数量$K$, 概率密度估计形式为:
\[p(x)=\frac{K}{NV}\]根据上式,可以有两种方式
- 固定$K$然后从数据中确定$V$, 这就是$K$近邻算法。
- 固定$V$,然后从数据中确定$K$,这就是核方法。
接下来介绍核方法。 \(k(u) = \begin{cases} 1 & \text{if $\mid u\mid<1/2, i=1,...,D$, } \\ 0 & \text{otherwise} \end{cases} \qquad(2)\) 上式称为Parzen窗, 也称为核函数。
如果数据点$x_n$位于以 $x$为中心的边长为$h$的立方体中,那么量$k(\frac{x-x_n}{h})$的值等于1,否则它的值为0. 于是位于这个立方体内的总数为:
\[K=\sum_{n=1}^{N}k(\frac{x-x_n}{h})\]从而得到$x$点的概率密度:
\[p(x)=\frac{1}{N}\sum_{n=1}^{N}\frac{1}{h^D}k(\frac{x-x_n}{h})\]其中$h^D$表示体积。
我们可以反过来理解。训练数据中落入以$x$为中心的立方体的数目等价于: x落入多少个以$x_n$的立方体之内。所以上面要计算某点$x$的概率密度,就是统计$x$落入几个正方体内,落入则累加1,从而获得总的落入数量。再除以总数量则获得概率密度。
在立方体边界会有不连续性。一般可以选用高斯核。核密度函数为:
\[p(x)=\frac{1}{N}\sum_{n=1}^{N}\frac{1}{(2\pi h^2)^{\frac{D}{2}}}exp\{-\frac{\Vert x-x_n \Vert^2}{2h^2}\}\]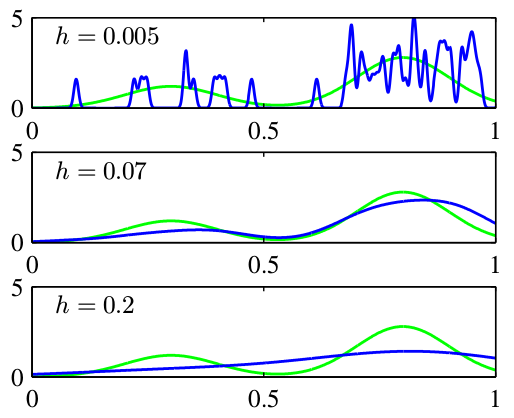
上图表示,小的$h$对噪声敏感,大的$h$过于平滑。
在p91页中,核方法只是用来估计p(x) 概率密度. 在直方图中是有一定的表现能力的。但如何应用在其他场景?
2. 核方法
这部分对应prml第六章
训练数据点或者它的一个子集在预测阶段仍然保留并且被使用。memory_based。
输入$x$可以经过基函数$\phi(x)$映射到固定非线性特征空间。核函数可以表示为:
\[k(x, x')=\phi(x)^T\phi(x')\]所有算法如果输入$x$只以内积形式出现,则可以用核来替换。称为核技巧。
kernel pca
2.1 对偶
许多回归的线性模型和分类的线性模型的公式都可以使用对偶表示重写。使用对偶表示形式, 核函数可以自然地产生。对偶公式使得最小平方问题的解完全通过核函数$k(x, x’)$表示。这被称为对偶公式。通过正常的推导,引出了核函数。
考虑线性模型其参数通过最小化正则化平方和误差来确定:
\[J(w)=\frac{1}{2}^2+\frac{\lambda}{2}w^Tw\]令关于$w$梯度为0,得到:
\[w=-\frac{1}{\lambda}\sum_{n=1}^{N}{\{w^T\phi(x_n)-t_n\}}\phi(x_n)=\sum_{n=1}^{N}a_n\phi(x_n)=\Phi^T\mathbf a \qquad(6.3)\]其中$\Phi$是设计矩阵,第n行为$\phi(x_n)^T$. 向量$\mathbf a=(a_1, …,a_N)^T$, 并且,
\[a_n=-\frac{1}{\lambda}{\{w^T\phi(x_n)-t_n\}}\phi(x_n) \qquad(6.4)\]
gram。与neural style的gram关系?
对偶公式的优点是,它可以完全通过核函数$k(x,x’)$来表示。于是,我们可以直接针对核函数进行计算,避免了显式地引入特征向量$\phi(x)$ ,这使得我们可以隐式地使用高维特征空间,甚至无限维特征空间。
2.2 构造核
构造核的方式:
-
选择一个特征空间映射 φ(x) ,然后使用这个映射寻找对应的核
-
直接构造核函数
下面对于直接构造核函数的例子,
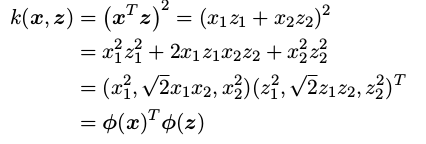
特征映射函数为: $\phi(x)=(x_1^2, \sqrt{2}x_1x_2, x_2^2)^T$
可以通过组合简单核函数获得复杂核函数,这里不细讲。
2.2.1 生成式
[todo]构造核的另一个强大的方法是从一个概率生成式模型开始构造?
2.2.2 fisher核
todo
2.3 径向基函数网络
径向基函数: 每一个基函数只依赖于样本核中心$u_j$之间的径向距离。即$\phi(x)=h(|x-u_j|)$
径向基函数被用来进行精确的函数内插。 给定一组输入向量${x_1, …,x_n}$ 以及对应的目标值$t_1,…,t_n$ ,目标是找到一个光滑的函数$f(x)$, 使得其能精确拟合每一个目标值。
\[f(x)=\sum_{n=1}^{N}w_nh(\|x-x_n\|)\]其中系数$w_n$的值由最小平方方法求出。
由于具有与系数相同的限制条件,因此能够精确拟合每一个目标函数(即方程数目和未知数数目相等,所以可以求得唯一解)。但是,通常目标值带有噪声,精确内插反而不是我们想要的,因为这通常意味着过拟合。
2.3.1正则化理论
2.3.2 Nadaraya-Watson 模 型
3.3.3节回顾。
参数分布
prml中文版p112,p116等价核
先验:
\[p(w)=N(w\mid m_0,S_0)\]其中$m_0$是均值,$S_0$是协方差。
后验分布:
\[p(w\mid t)=N(w\mid m_N, S_N)\]其中
\[m_N=S_N(S^{-1}m_0+\beta\Phi^Tt)\] \[S_N^{-1}=S_0^{-1}+\beta\Phi^T\Phi\]为了简单,考虑零均值,各向同性高斯分布。这个分布有精度$\alpha$控制。即:
\[p(w\mid \alpha)=N(w\mid 0, \alpha^{-1}I)\]这时候,
\[m_N=\beta S_N\Phi^Tt \qquad(3.53)\] \[S_N^{-1}=\alpha I+\beta\Phi^T\Phi\]等价核
公式(3.53)给出的线性基函数模型的后验均值解有一个有趣的解释,这个解释为核方法 (包括高斯过程)提供了舞台。
将公式3.53代入$y(x,w)=w^T\phi(x)$得到:
\[y(x,m_N)=m_N^T\phi(x)=\beta \phi(x)^T S_N \Phi^Tt=\sum_{n=1}^{N}\beta \phi(x)^T S_N \phi(x_n)t_n\]因此,在点$x$处的预测均值由训练集目标变量$t_n$的线性组合给出。即,
\[y(x,m_N)=\sum_{n=1}^{N}k(x,x_n)t_n \qquad(3.61)\]其中, 函数
\[k(x,x')=\beta \phi(x)^TS_N\phi(x') \qquad(3.62)\]称为平滑矩阵或等价核。
上式可以转化为内积形式。$k(x,z)=\psi(x)^T\psi(z)$
其中
\[\psi(x)=\beta^{\frac{1}{2}}S_N^{\frac{1}{2}}\phi(x)\]Nadaraya-Watson:
在3.3.3节中,对于新的输入$x$ ,线性回归模型的预测的形式为训练数据集的目标值的线性组合,组合系数由等价核(公式3.62)给出。其中等价核满足加和限制$\sum_{n=1}^{n}k(x, x_n)=1$。
我们从核密度估计开始,以一个不同的角度研究回归模型(公式3.61). 假设有训练集${x_n, t_n}$, 使用Parzen密度估计来对联合分布$p(x,t)$进行建模, 即
\[p(x,t)=\frac{1}{N}\sum_{n=1}^{N}f(x-x_n, t-t_n)\]其中,$f(x,t)$是分量密度函数,每个数据点都有一个以该数据点为中心的这种分量。

(另一个展开归一化径向基函数的情况是把核密度估计应用到回归问题中,正如我们将在6.3.1节讨论的那样)
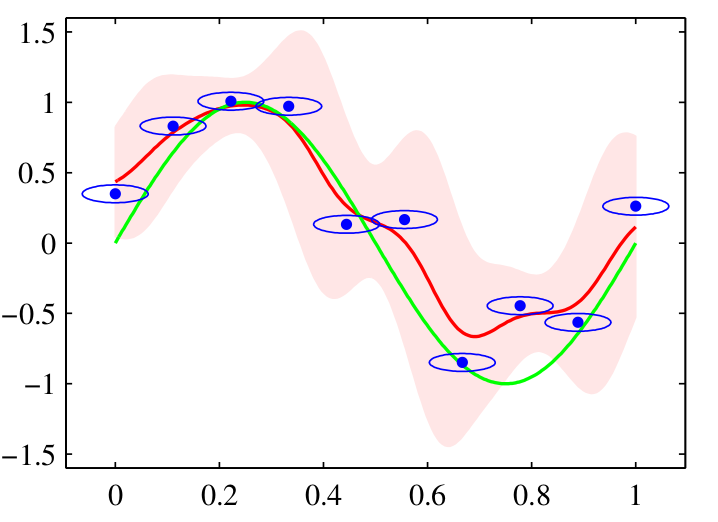
使用各向同性的高斯核的 Nadaraya-Watson 核回归模型的说明。数据集为正弦数据集。原始的正弦 函数由绿色曲线表示,数据点由蓝色的点表示,每个数据点是一个各向同性的高斯核的中心。得到的回 归函数,由条件均值给出,用红线表示。同时给出的还有条件概率分布 p(t|x) 的两个标准差的区域,用 红色阴影表示。在每个数据点周围的蓝色椭圆给出了对应的核的一个标准差轮廓线。由于水平轴和垂直 轴的标度不同,这些轮廓线似乎不是圆形的。
3. 高斯过程
详细例子
4. svm
prml第7章, pluskid博客
svm对偶问题为什么有个max,为什么更高效。kkt的具体影响怎么实现的
稀疏核机
4.1 线性可分
距离推导
4.2 对偶形式
对偶形式不但使得计算更加高效,同时产生了内积形式。从而可以使用核技巧。(偷吃步)
原本minmax问题。min是目标函数最小化,max是拉格朗日不等式。但是在这种情况下,max插在其中,没有办法通过变量替换的方式,转化成内积形式,从而使用核技巧。理论上,在满足kkt条件下,minmax可以转化成max min的方式。这样就可以进行变量替换了 在min的时候,通过求导,可以获得w的变量替换,和一个约束条件。将约束条件并入max中,并且进行变量替换,可以消去min。 这样就只要求max了
kkt条件
4.3 核
4.4 soft margin

形式
合页损失函数
4.5 smo求解
5 机器学习技法笔记

在核技巧这节讲到核方法其实就是偷吃步。在这个例子中,原本要求x的转换后的内积。需要先转换到特征空间中,这个特征空间可能很多维。而通过核方法,可以把这个过程直接使用一个原始空间的一个核函数计算出来,不用管转换后的空间是什么。这样就大大提高了计算效率。这个例子由于基函数只有两阶,所以难度加速不够明显,更高阶的话,基函数的计算更复杂,使用核方法的收益也就越高

在kernel svm中,将w表示为z,从而出现内积形式。使用核方法进行偷吃步。
完整kernel svm如下

更高阶的多项式核
prml p295是关于这个式子更简单的例子。
高斯核
高斯核通过泰勒展开可以转化为向量内积的形式。

高斯核的内在意义是在获取支撑向量边界上点的高斯分布的线性组合,使得在无穷多维上获得最大分隔边界

参考
http://blog.pluskid.org/?page_id=683 prml
prml中文版 马春鹏
机器学习 周志华
统计学习方法 李航 mlapp 机器学习技法 林轩田