- 第一课:代码配置
- 第二课:简单画图
- 第三课 MVP矩阵
- 第四课:
- 第五课:纹理立方体
- 第六课:简单控制
- 第七课:模型加载
- 第八课:光照
- 第九课:index VBO
- 第十课:透明
- 第十一课: 文字输出
- 第十三课: Normal Mapping(法线贴图)
- 第十四课:render to texture(贴图烘培)
原文见这里
第一课:代码配置
第二课:简单画图
GLuint VertexArrayID;
glGenVertexArrays(1, &VertexArrayID);
glBindVertexArray(VertexArrayID);
创建一个顶点数组对象,并将它设为当前对象。当窗口创建成功后(即OpenGL上下文创建后),马上做这一步工作;必须在任何其他OpenGL调用前完成。(VAO)
第三课 MVP矩阵
齐次坐标,MVP矩阵关系,变化,推导

第四课:
OpenGL的缓冲区由一些标准的函数(glGenBuffers, glBindBuffer, glBufferData, glVertexAttribPointer)来创建、绑定、填充和配置;
第五课:纹理立方体
给一个模型贴纹理时,需要通过某种方式告诉OpenGL用哪一块图像来填充三角形。这是借助UV坐标来实现的。将三维坐标映射到uv坐标。就像是将正方形拆开。自己可以决定拆开的方式 每个顶点除了位置坐标外还有两个浮点数坐标:U和V。这两个坐标用于获取纹理。 对应于obj文件的纹理坐标。 为了抗锯齿,需要用最近邻,线性,线性等插值方法。但是所有这些方法在远处看过去可能颜色混合不够。这时候需要mipmap技术

一开始,把图像缩小到原来的1/2,然后依次缩小,直到图像只有1×1大小(应该是图像所有纹素的平均值) 绘制模型时,根据纹素大小选择合适的mipmap。 可以选用nearest、linear、anisotropic等任意一种滤波方式来对mipmap采样。 要想效果更好,可以对两个mipmap采样然后混合,得出结果。
glGetUniformLocation: 用于定义uniform变量
第六课:简单控制
根据鼠标键盘的操作重新计算出viewMatrix。主要是lookat参数的确定,主要包括:position,direction,up
视线方向:
glm::vec3 direction(
cos(verticalAngle) * sin(horizontalAngle),
sin(verticalAngle),
cos(verticalAngle) * cos(horizontalAngle)
);

右方向: 右方向于y无关,故y为0。 且竖直方向的旋转不会影响y,只需要考虑水平方向的旋转。计算方法与二维相同。
glm::vec3 right = glm::vec3(
sin(horizontalAngle - 3.14f/2.0f),
0,
cos(horizontalAngle - 3.14f/2.0f)
);
由前和右叉乘出向上的方向:
glm::vec3 up = glm::cross( right, direction );
第七课:模型加载
obj文件格式:
注释标记#。usemtl和mtlib描述了模型的外观。本课用不到。
v代表顶点
vt代表顶点的纹理坐标
vn代表顶点的法向
f代表面
8/11/7描述了三角形的第一个顶点
7/12/7描述了三角形的第二个顶点
6/10/7描述了三角形的第三个顶点
对于第一个顶点,8指向要用的顶点。此例中是-1.000000 1.000000 -1.000000(索引从1开始,和C++中从0开始不同) 11指向要用的纹理坐标。此例中是0.748355 0.998230。 7指向要用的法线。此例中是0.000000 1.000000 -0.000000。
第八课:光照
一个平面的法向是一个长度为1并且垂直于这个平面的向量。
triangle ( v1, v2, v3 )
edge1 = v2-v1
edge2 = v3-v1
triangle.normal = cross(edge1, edge2).normalize()
引申开来:顶点的法向,是包含该顶点的所有三角形的法向的均值。
float cosTheta = dot(normal, light);
float cosTheta = clamp(dot(normal, light), 0, 1); //防止光源在背后
color = LightColor * cosTheta
color = MaterialDiffuseColor * LightColor * cosTheta; //考虑材质颜色
取得取得方向量,光照最后在着色器里面进行计算。片段着色器最终就是为了获得颜色color
顶点着色器:
// Vector that goes from the vertex to the camera, in camera space.
// In camera space, the camera is at the origin (0,0,0).
vec3 vertexPosition_cameraspace = ( V * M * vec4(vertexPosition_modelspace,1)).xyz;
EyeDirection_cameraspace = vec3(0,0,0) - vertexPosition_cameraspace;
// Vector that goes from the vertex to the light, in camera space. M is ommited because it's identity.
vec3 LightPosition_cameraspace = ( V * vec4(LightPosition_worldspace,1)).xyz;
LightDirection_cameraspace = LightPosition_cameraspace + EyeDirection_cameraspace;
// Normal of the the vertex, in camera space
Normal_cameraspace = ( V * M * vec4(vertexNormal_modelspace,0)).xyz;
片段着色器:(在相机空间进行)
vec3 n = normalize( Normal_cameraspace );
vec3 l = normalize( LightDirection_cameraspace );
float cosTheta = clamp( dot( n,l ), 0,1 );
vec3 E = normalize(EyeDirection_cameraspace);
vec3 R = reflect(-l,n);
float cosAlpha = clamp( dot( E,R ), 0,1 );
color =
// Ambient : simulates indirect lighting 环境光
MaterialAmbientColor +
// Diffuse : "color" of the object 漫反射
MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) +
// Specular : reflective highlight, like a mirror 镜面光
MaterialSpecularColor * LightColor * LightPower * pow(cosAlpha,5) / (distance*distance);
这个着色模型得益于其简单性,已经使用多年。但它存在很多问题,因而被microfacet BRDF(bidirectional reflection distribution function,微表面双向反射分布函数)之类的基于物理的(physically-based)模型所取代
第九课:index VBO
索引缓冲存储的是整数;每个三角形有三个整数索引,分别指向各种属性缓冲(attribute buffer)顶点位置、颜色、UV坐标、其他UV坐标、法线缓冲法线等)。这和OBJ文件格式有些类似,但一个最大的区别在于:索引缓冲只有一个。这也就是说仅当某顶点的所有属性(译注:即位置、颜色、UV坐标、法线等等)在两个三角形中都相同时,我们才认为此顶点是两个三角形的公共顶点。
索引 代码中同时展示了显示多个object的方法。主要是对modelMatrix进行重新赋值
第十课:透明
处理透明的解决方案:不用排序, 避免性能影响
第十一课: 文字输出
将点转换到UV 为什么除以16?
第十三课: Normal Mapping(法线贴图)
为什么叫法线贴图,我们知道法线(Normal)是垂直于一个面的直线,通过计算光线与这条法线的角度就可以知道与面的角度,进而可以计算出面应得到的颜色值。如果我们知道物体每个面的法线就能实现对这个物体进行光照渲染。但是一堵墙也许只有四个顶点,也就是只有一个面,它最终的渲染效果将会非常单一,假设这堵墙上有更多的砖的凹凸痕迹,我们怎样实现仅用四个顶点渲染出立体感很强,细节层次感很强的这堵墙呢,答案就是 法线贴图(Normal Map)。 在法线贴图技术中,我们就是通过把墙面的每个像素的法线存储在一张纹理中,渲染的时候根据每个像素的法线确定他们的阴暗程度,而这张法线贴是可以用photoshop软件从一张墙的纹理生成对应的法线贴图的。到此,熟悉法线贴图的朋友会对以上内容很熟悉的。 试想在渲染过程中,如果把每个法向量都转换到世界空间中跟光向量计算角度的话,那么这么多的像素法向量肯定影响性能,但是如果把光向量转换到法向量所在的空间中,岂不快哉?因此我们这里提到一个正切空间(Tangent Space)。正切空间就是法向量所在的空间,在这个坐标系中,法向量作为高度轴,类似Z轴。再找到其他的两个轴问题就会变得简单,但恰好这里是比较麻烦的。 其实我们已经知道 高度轴了,再找到一个轴,第三个轴就可以通过已知的两个轴做叉乘得到。我们要找的那个轴就叫做 正切向量(Tangent Vector)。正切向量是需要平行于法向量的平面的。(这里不是用这个??) 切线方向的选择:选择与纹理坐标系相同的方向(下图红线). 绿线是另一条切线:bitangent(双切线)
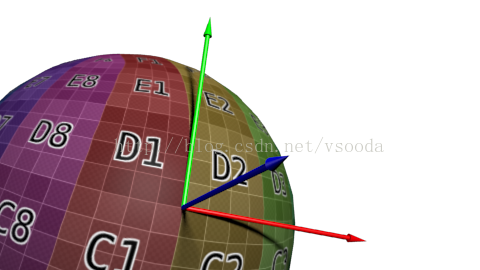
截至目前,每个顶点仅有一条法线。在三角形内部,法线是平滑过渡的,而颜色则是通过纹理采样得到的(译注:三角形内部法线由插值计算得出,颜色则是直接从纹理取数据)。法线贴图的基本思想就是像纹理采样一样为法线取值。法线纹理的映射方式和漫反射纹理相似。麻烦之处在于如何将法线从各三角形局部空间(切线空间tangent space,亦称图像空间image space)变换到模型空间(着色计算所采用的空间)。
切线计算:
已知在UV上的坐标deltaUV1, deltaUV2. 那么
deltaPos1 = deltaUV1.x * T + deltaUV1.y * B
deltaPos2 = deltaUV2.x * T + deltaUV2.y * B
float r = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV1.y * deltaUV2.x);
glm::vec3 tangent = (deltaPos1 * deltaUV2.y - deltaPos2 * deltaUV1.y)*r;
glm::vec3 bitangent = (deltaPos2 * deltaUV1.x - deltaPos1 * deltaUV2.x)*r;
正交化: 顶点着色器中,为了计算速度,我们没有进行矩阵求逆,而是进行了转置。这只有当矩阵表示的空间正交时才成立,而这个矩阵还不是正交的。好在这个问题很容易解决:只需在computeTangentBasis()末尾让切线与法线垂直。
t = glm::normalize(t - n * glm::dot(n, t));
这里之所以可以直接计算出T,N是因为世界坐标上的点与uv上的点已经有一一对应关系。 有了TBN矩阵, 通常我们将模型空间变换到切线空间。
顶点着色器:
vec3 vertexTangent_cameraspace = MV3x3 * vertexTangent_modelspace;
vec3 vertexBitangent_cameraspace = MV3x3 * vertexBitangent_modelspace;
vec3 vertexNormal_cameraspace = MV3x3 * vertexNormal_modelspace;
mat3 TBN = transpose(mat3(
vertexTangent_cameraspace,
vertexBitangent_cameraspace,
vertexNormal_cameraspace
)); // You can use dot products instead of building this matrix and transposing it. See References for details.
LightDirection_tangentspace = TBN * LightDirection_cameraspace;
EyeDirection_tangentspace = TBN * EyeDirection_cameraspace;
片段着色器:
vec3 n = TextureNormal_tangentspace;
vec3 l = normalize(LightDirection_tangentspace);
float cosTheta = clamp( dot( n,l ), 0,1 );
vec3 E = normalize(EyeDirection_tangentspace);
vec3 R = reflect(-l,n);
float cosAlpha = clamp( dot( E,R ), 0,1 );
关于TBN空间的理解:已知一个三角形在模型空间的三维坐标,同时知道在uv上的坐标。模型空间和uv空间成投影关系。现在所求的T,B是空间上的两个坐标轴(这两个坐标轴即为投影平面),使得uv上的变化能完整体现在三维模型空间。通过公式求出T,B之后,此时N不一定垂直于这两者构成的空间(取决于三维坐标和uv坐标的关系),所以需要进行正交化。 最后一个切线空间上的坐标(a, b, c), 其在模型空间上的表示直接就是:a* T + b * B + c * N;
第十四课:render to texture(贴图烘培)
We have three tasks : creating the texture in which we’re going to render ; actually rendering something in it ; and using the generated texture.
贴图烘焙技术也叫Render To Textures,简单地说就是一种把max光照信息渲染成贴图的方式,而后把这个烘焙后的贴图再贴回到场景中去的技术。这样的话光照信息变成了贴图,不需要CPU再去费时的计算了,只要算普通的贴图就可以了,所以速度极快。由于在烘焙前需要对场景进行渲染,所以贴图烘焙技术对于静帧来讲意义不大,这种技术主要应用于游戏和建筑漫游动画里面,这种技术实现了我们把费时的光能传递计算应用到动画中去的实用性,而且也能省去讨厌的光能传递时动画抖动的麻烦。