随机森林是有多颗决策树组成的。由于其速度快,效果好,在很多kaggle等很多大数据竞赛中,取得非常好的结果。随机森林被认为代表集成学习水平的方法。
样例
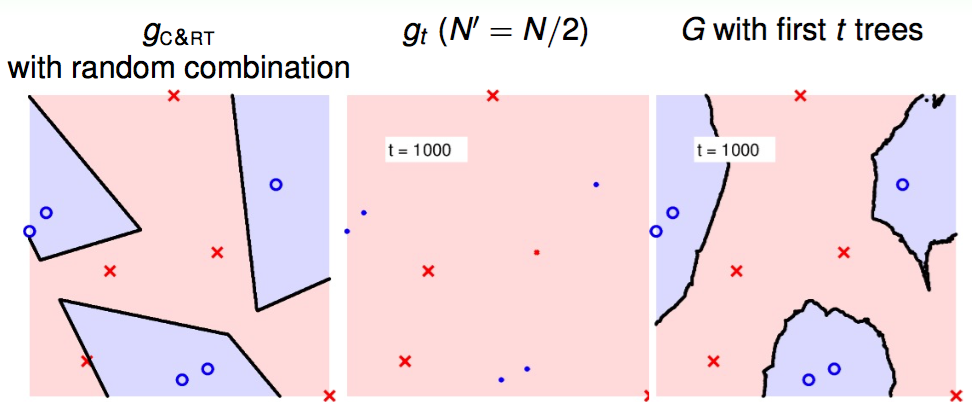
图1,2,3分别是单棵决策树,100棵决策树,1000棵决策树的分类结果。在每张图中左图为决策树分类结果;中图为采样N/2个样本后使用决策树分类结果;右图是多个采样的决策树联合的结果。1


随机森林原理

basis vs variance
泛化误差可以分解为偏差(basis),方差(variance),噪声之和。噪声是常数。2
在训练不足时,学习期的拟合能力不够强,训练数据的扰动不足以使得学习器产生显著的变化,此时偏差主导了泛化错误率。
随着训练程度的加深,学习器的拟合能力逐渐增强,训练数据的扰动渐渐能被学习器学到,方差逐渐主导了泛化错误率。在训练充足之后,学习器的拟合能力比较强,训练数据的轻微扰动都会导致学习器发生显著的变化。若训练数据自身的,非全局的特性被学习器学到了,则将发生过拟合。
bagging vs boosting
Bagging:Bootstrap AGGregatING
bagging和boosting都是通过学习大量的弱分类器,再将其组合起来,构成强分类器。
boosting训练的弱分类器的训练是通过对前面调整分类错误样本的权重达到的。bagging的通过对样本的重采样从而训练得到不同的分类器。
boosting主要关注的是降低偏差。因此boosting能基于泛化性能相当弱的学习器构建出很强的集成。bagging主要关注降低方差,因此在不剪枝的决策树,神经网络等易受样本扰动影响的学习器上取得很好的效果。
属性选择
- 随机属性选择 在决策树的属性集合(假定有d个属性)中随机选择一个包含\(k\)个属性的子集,再从中选择最好的属性用于划分。\(k=log_2d\)
- 属性投影
多个属性组合
oob(包外估计)
oob: out-of-bag estimate
\[(1-\frac{1}{N})^N\approx\frac{1}{e}\]有放回采样,采样N次,则一次都没有被选中的概率大约是1/3. 这些大量的样本可以作为验证集。

其中\(G_n^-\)是那些不包含\(x_n\)的决策树。用那些树来验证分类器在数据集上的对于\(x_n\)的分类错误。
\[G_n^-(x_n)=average(g_2,g_3,g_T)\]属性裁剪
如果有很多属性,有冗余。比如说,年龄和生日。要将其中冗余属性去掉,留下真正对训练有用的属性。例如原本有10000个属性,需要选择300个。
如果是线性模型,\(score=w^Tx=\sum_{i=1}^{d}w_ix_i\), \(w\)越大,代表其重要性更大。
对于非线性模型一般使用Permutation Test 测试属性重要的方法是,在该属性上去一个错误的值,如果正确率不受影响,那么说明该属性是不必要的。如果正确率收到较大影响,则保留该属性。
改变属性值的方法:如果通过对某个属性的取值加上一个随机数,那么不仅该属性的值变化,其分布也跟着变化。这样不利于评估最终结果。在统计学上,一般是讲不同样本的对应属性进行交换,这个每个属性的取值变化了,但是其分布不变。