在hmm基于最大似然(ML)的聚类策略,很难确定最终停止条件。mdl自动判别最终聚类停止条件,在很多情况下取得很好的结果。
Shinoda K, Watanabe T. MDL-based context-dependent subword modeling for speech recognition[J]. The Journal of the Acoustical Society of Japan (E), 2000, 21(2): 79-86.
1. mdl criterion
假如有一组模型\(\{1,2,…,i,…,I\}\). 对于数据\(\{x^N=x_1,…,x_N\}\),其描述长度为\(l_i(x^N)\),在模型\(i\)的描述长度表示为:
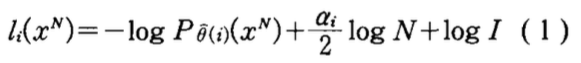
上式右边三项分别为:
- 第一项:数据\(x^N\)在模型\(i\)下的最大似然概率的负log值。最大似然概率越大,其负log值越小。所以,这一项随着结点的分裂,越来越小。
- 第二项:对于模型复杂度的惩罚项,模型越复杂,这个值越大。
- 第三项: 常数,可忽略。
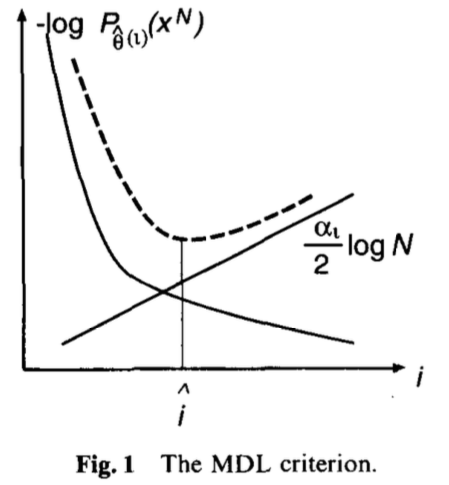
mdl计算时,就是要需找一个模型使得描述长度\(l_i(x^N)\)最小。第一项与第二项和最终优化目标的关系如下图所示。第一项越来越小,第二项越来越大。找一个点,使得两者的和最小。
###2. description length for HMMs 对于包含\(E\)个句子(example)的数据,每个句子\(e\)内部的数据表示为\(\{o_1^e,…,o_t^e,…,o_{T_e}^e\}\),其中\(T_e\)是句子\(e\)的帧数。
- hmm 均值,协方差
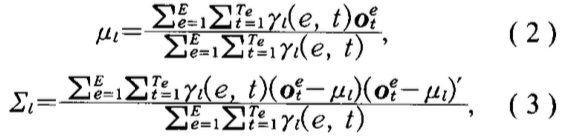
- \(e\)句子,第\(t\)帧属于状态\(s_t\)的概率\(\gamma_l(e,t)\)表示如下
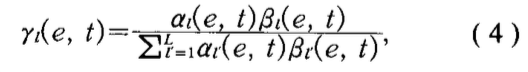
-
计算所有结点集合的似然概率计算代价太高,所以做了以下假设:
- 在计算似然概率时,忽略转移概率
- 状态集合的分裂,不改变帧和状态的对齐关系
- 一个状态产生数据序列o的似然概率可以表示为:各个数据点属于该状态的概率乘上高斯分布产生该数据的概率的似然值之和。这个假设是合理的原因在于,公式4中,每个样本属于某个状态的值,参考了其前向概率和后向概率。综合前后概率之后,会导致基本大部分\(\gamma_l(e,t)\)的值为0,只有真实状态的概率接近为1
-
在三音素模型集合中,将属于同一个结点的模型当做一个模型子集。例如\(\{s_1^m,…s_l^m,…,s_{L_m}^m\}\)构成了结点\(S_m\),而\(L_m\)是状态子集中状态个数。所有状态可以重新按照其子集标记为:\(\{s_1^1,…,s_{L_1}^1,s_1^m,…,s_{L_m}^m,s_1^m,…,s_{L_M}^M\}\)。公式2,3可以重写为:
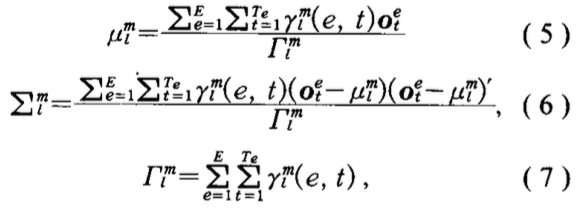
- 在第二个假设下,结点集的均值方差计算为
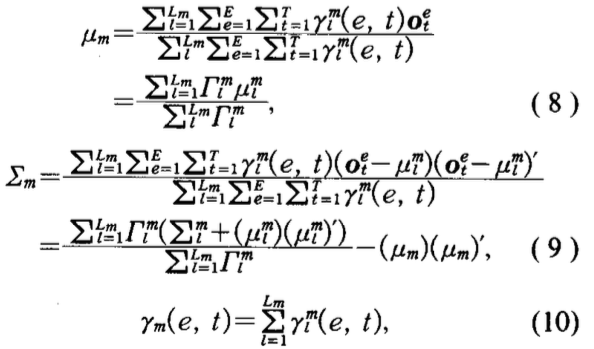
- 在第三假设下,由\(s_m\)产生数据\(\{o_1,…,o_t,…,o_{T}\}\)的log似然概率为:
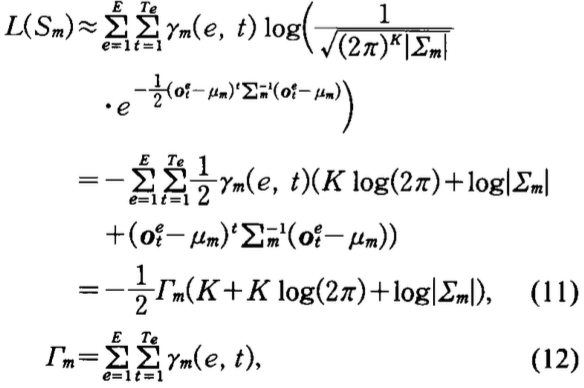
其中\(K\)是观测数据的维度,\(\Gamma_m\)表示状态集\(S_m\)总的出现次数。
- 数据集对于状态集合\(U\)的log似然函数表示为:
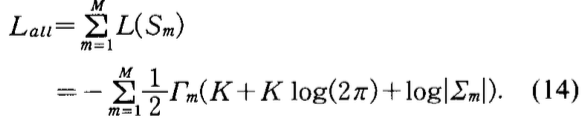
- 公式1右边第二项模型复杂度惩罚表示为:
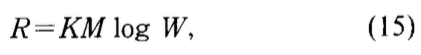
其中\(W=\sum_{m=1}^M\Gamma_m\)
- 公式1最终转化为
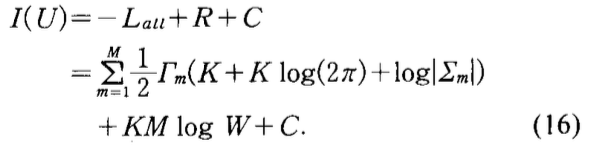
最后一项\(C\)是常数。
基于mdl进行状态集分裂
- 假设\(U\)状态中结点\(S_m\)对于问题\(q\)分裂为\(S_{mqy}\)和\(S_{mqn}\),分裂后集合记为\(U^{\prime}\).
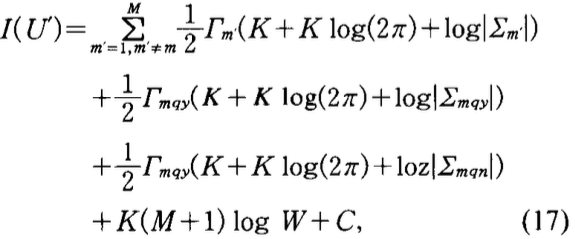
注意分裂之后,结点数目标为\(M+1\), 所以上式模型惩罚项中更改惩罚系数。
- 用\(\Delta_m(q)\)表示分裂前后描述长度的差。
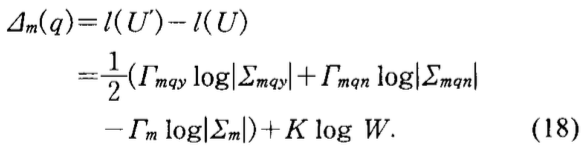
在分裂时候,首先选取一个问题\(q^{\prime}\),使得\(\Delta_m(q^{\prime})\)最小。若\(\Delta_m(q^{\prime})>0\),则不分裂。若\(\Delta_m(q^{\prime})<0\)则分裂。并递归分裂下去,直到无法分裂为止。
- 作为对比,在ML方法中,使用\(\delta_m(q)\)来表示状态\(S_m\)按照问题\(q\)划分为\(S_{mqy}\)和\(S_{mqn}\)后的log似然概率的提升值。
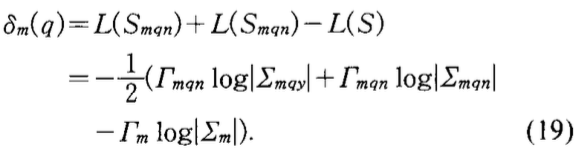
在该方法中,同样先找到一个\(q^{\prime}\),使得\(\delta_m(q^{\prime})\)最大。在找到这个问题\(q^{\prime}\)需要决定是否划分。因为划分总是会使得似然概率变大,需要外部条件来帮助确定是否停止划分。常用的条件是:设定log似然概率最小增长阈值或样本最小出现次数\(\Gamma_m\)阈值.
- 权重
为了调节公式1右边第一项和第二项权重,增加一个因子\(c\)进行调节
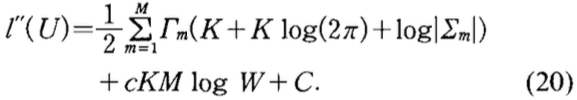
discussion
- 不确定三个假设的影响
- 不一定是最优的
- 最短描述长度未必是效果最好的
相对于ML方法最大的好处是不需要手动调节停止条件。
个人理解
文章认为结点划分一定会使得似然概率的值增大的原因在于: 公式4中,每个样本属于某个状态的值,参考了其前向概率和后向概率。综合前后概率之后,会导致基本大部分\(\gamma_l(e,t)\)的值为0,只有真实状态的概率接近为1。也就是说,在结点划分之后,会使得左右两个结点的纯度更高,当然也就使得似然概率更大了。