tts tutorial

• 1 介绍
• 2 基于hmm的参数语音合成
  • 2.1 文本特征构造
  • 2.2 模型训练
    • HMM模型 Baum-Welch训练
    • Viterbi training（forced alignment）
    • context-dependent model和状态绑定
    • duration模型和hsmm
  • 2.3 mlpg gv 参数生成
    • mlpg
    • mlpg gv参数生成
  • 2.4 声码器
    • 2.4.1 参数定义
    • 2.4.2 D4C算法步骤
• 3 基于深度学习的参数语音合成
  • 3.1 时长模型
  • 3.2 声学模型
    • 3.2.1 vuv
    • 3.2.2 归一化
  • 3.3 预测
  • 3.4 网络模型
    • 3.4.1 dnn
    • 3.4.2 rnn
• 4 adapt技术
  • 4.1 基于HSMM的MLLR
  • 4.2 平均音模型（Average Voice Model）
  • 4.3 说话人自适应训练（SAT）
  • 4.4 dnn adapt
    • 4.4.1 ivector提取
    • 4.4.2 ihuc
    • 4.4.3 feature space map
• ５ 基于生成模型的语音合成
  • wavenet
    • 5.1 wavenet
    • 5.2 Causal Convolutional Layer
    • 5.3 Dilated Causal Convolutional Layer
    • 5.4 Gated Activation Unit && Residual and Skip Connections
    • 5.5 音频数据量化
    • 5.6 wavelet在TTS中的应用
  • char2wav
  • sampleRnn

本文将从传统基于拼接的语音合成，基于参数的语音合成讲到最新基于生成模型的语音合成。参数生成部分由于jimmy完成，声码器部分由lbq完成，wavenet部分由于mingAn完成.

1 介绍

传统的语音合成一般有两种做法。一种是基于波形拼接的，一种是基于参数合成的。

所谓波形拼接就是准备大量的不同情感不同语境的语音数据，在拼接的时候选取最适合的单元。单元拼接的算法的好处在于音质较高，声音还原度高。单元挑选的缺点在于需要大量的数据，合成不够灵活，没有办法做一些情绪变化。当无法挑选到满意单元的时候，会使得衔接及其不自然。而且模型较大，没有办法离线。

基于参数的语音合成指的是，构造上下文文本特征作为输入，再通过特征抽取获得语音数据的声学特征作为输出。用hmm或者dnn等算法学习输入到输出的映射关系。有了这个映射关系之后，对于任意输入文本，提取其文本特征后，就可以得到声学特征。再将声学特征输入到声码器，从而合成语音。基于参数的语音合成的好处在于模型较小，需要的数据量较少，而且可以很容易的对参数进行微调，从而得到不同的合成效果。缺点在于，声音是通过声码器得到的，音质会有所损失，情绪比较不饱满，对于一些声色较特殊的语音，设置没有办法还原。

基于生成模型的语音合成指的直接合成波形上每个点的采样值。因为没有通过声码器，所以不会有音质损失。但由于每秒需要预测几千甚至几万个值，所以时间效率较低。

基于波形拼接的语音合成不符合我们的使用场景，下面主要介绍基于参数和基于生成模型的语音合成。

2 基于hmm的参数语音合成

下图是基于hmm参数语音合成的整体流程。

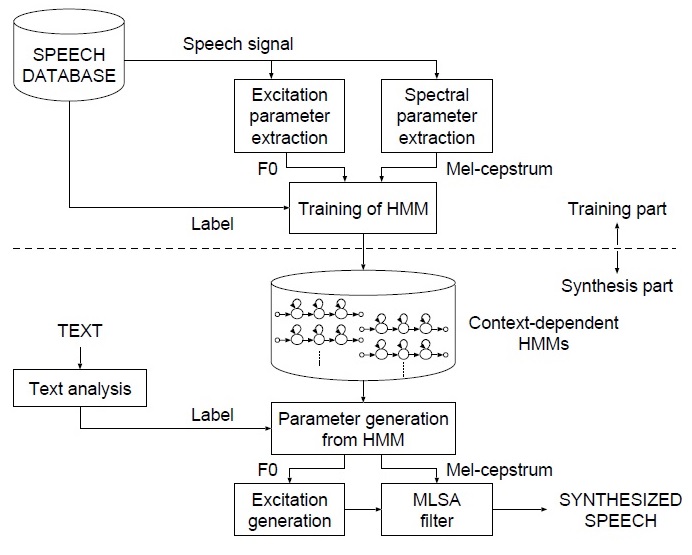
语音合成需要提取F0和mfcc等声学特征，并对文本提取标注信息，从而训练HMM模型。 对于新的句子，需要先提取标注信息，再输入到HMM模型中，或者声学参数（F0，mfcc）等，再通过STRAIGHT，WORLD等声码器算法，将这些参数还原为声音。参考¹

2.1 文本特征构造

我们人类说话的时候，对于同一个字在不同的情绪、不同上下文，发音也会有所不同。所以构造文本特征我们需要考虑: 上下文音素，句子长度，音素个数，句中位置，词组长度，词组位置，前后是否断句，情感如何，有没有特殊的转调规则，停顿如何等因素。

具体而言：

• 上下文音素: 考虑前面两个音素，当前音素，以及后面两个音素

• 词

  • 句子总共多少词
  • 词组总共多少词
  • 在句子中的位置
  • 在词组中的位置

• 音素

  • 句子总共多少音素
  • 词组总共多少音素
  • 在句子中的位置
  • 在词组中的位置

• 情感类别

• tobi信息

  • 升降调
  • 重读指数
  • 停顿指数

• 特殊转调规则

• 词性

  ​

2.2 模型训练

通常需要将文本先转化为发音单元，称为transcript。 最小的单元称为音素。现在通用的模型是把一个音素分为3个状态，分别用来模拟音素的开始、持续、结束。

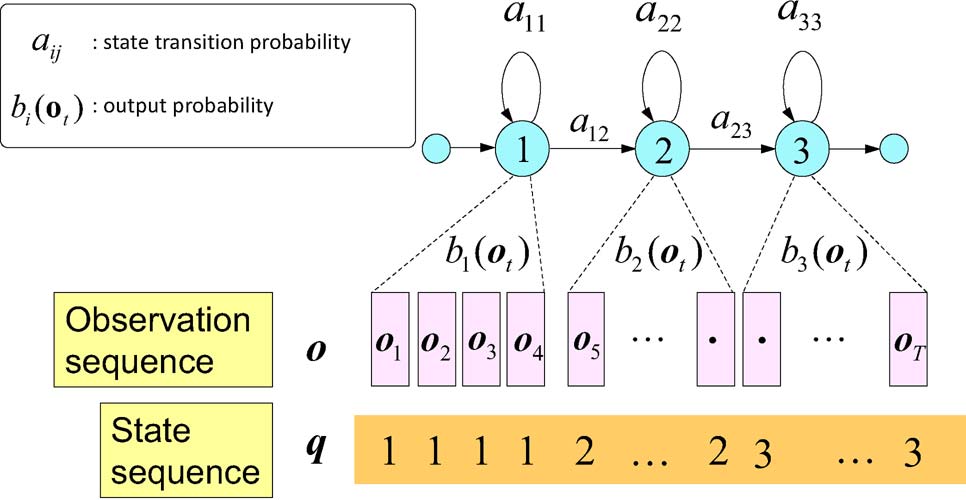
在声音序列中，将声音进行分帧。每帧对应一个状态。每个音素可能持续一定的时间， 所以上图中的q有重复的1，2，3表示每个状态的持续时间。（在htk中会将以上序列称为5状态hmm， 前后两个状态没有发射概率。中间三个状态标号分别为2，3，4）.

这里观测序序列除了包括F0， mfcc这些静态特征。还包括delta F0， delta delta F0 等动态特征。

在单音素hmm模型中，每个状态对应大量的观测值， 需要用个模型对状态到观测进行建模。一般选用多维高斯模型。之所以用多维，是因为观测值是多维的。 观测模型为：

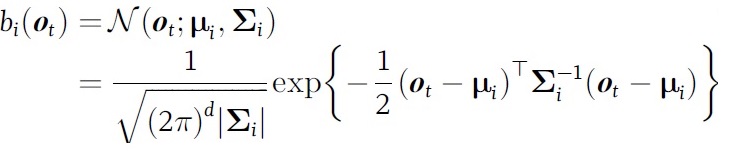
在训练和合成的时候:

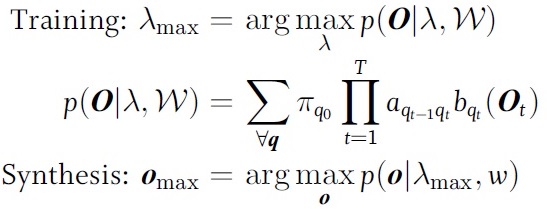
具体合成时:

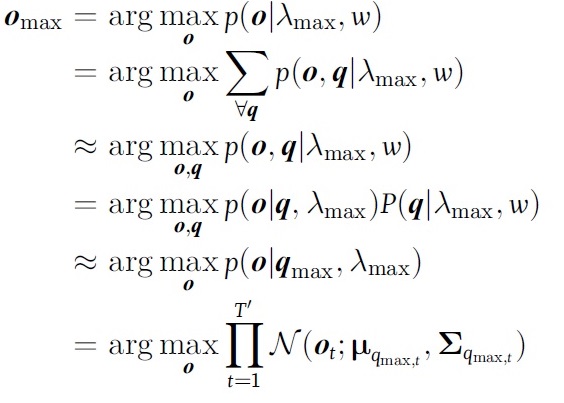
上面只是单个音素的模型，在句子中，通常的做法是将每个词对应的音素模型从左到右连接起来构造HMM网络。下图是a， i两个音素构造的hmm网络，在合成的时候需要决定:每个状态对应的观测，每个音素对应多少个状态（duration模型）。

HMM模型 Baum-Welch训练

在训练的时候，有的直接将整个词训练称为whole word模型；有的将词划分为音素再训练，则称为sub-word模型，这种训练也称为embeded training。参见² p7

Whole word模型将使用的整个词学习与声音的对应关系。最新基于深度学习的方法这样做取得不错的效果。HMM通常用的都是embeding training。 后文默认都指的是这种规模。 在上图中右图， 训练的初始化有两种方式， 一种是hInit + hres的方式，一种是HCompv的方式。第一种方式需要部分已经标注，对齐的数据。而第二种方式是我们通常使用的方式。即：将音素和观测训练按均匀等分的形式进行划分。然后使用全局的均值和方差作为每个音素模型的均值，方差。 这种初始化方法也成为flat-start。

对于观测模型：

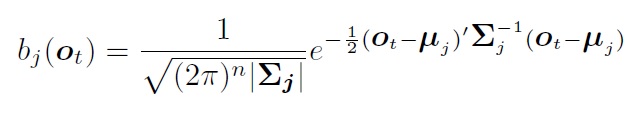
如果每个状态对应的观测值都已经标注好(对齐)， 那么直接可以求得均值和协方差：

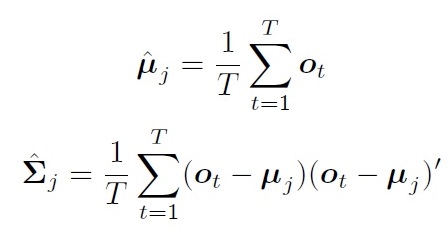
但是实际上，很难获得对齐数据。即使人工标注，也会容易造成不一致。

下面介绍通过Baum-Welch 训练算法.

在Baum-Welch 算法中，假设每个观测值都可以用任意状态产生。 将第t帧属于第j状态的概率标记为：\(L_j(t)\)

均值方差估计为：

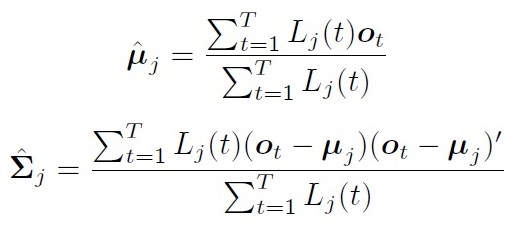
HMM前向算法：

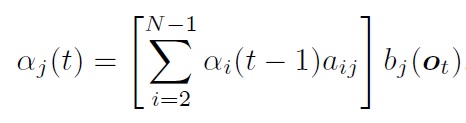
后向算法：

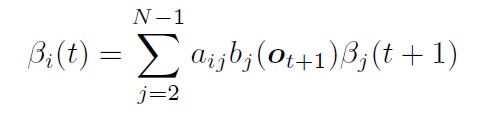
将第t帧属于第j状态的概率为：

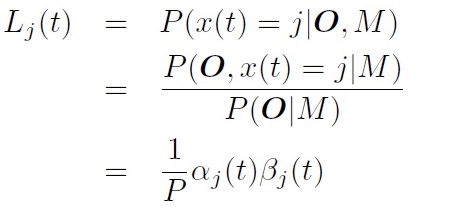
转移概率的更新比较复杂。需要分别计算进入概率，出去概率， 内部转移概率， 从入口直接到出口概率。参考² p135.

迭代以上过程，直到达到结束条件。（average log pro不再优化）

Viterbi training（forced alignment）

Baum-Welch training中，把每个观测值都可以由任意状态产生，通过概率控制其影响程度。称为软边界。而Viterbi training 中，寻找一个最佳路径，每个观测值只能属于一个状态，称为硬边界， 所以也成为forced alignment。

在上图中，对于一个给定的句子，其单词序列是固定的，包含哪些状态是固定的。只是需要寻找每个状态的持续时间（具体状态序列）。 而Baum-Welch training要先找到单词序列，才能找状态序列。从下图中可以看出，Viterbi算法对于某个观测值，要么属于当前状态，要么属于下一个状态，只有两个方向。而Baum-Welch training则需要考虑各种可能，所以Baum-Welch更耗时。参见³

到目前为止，最基本的 hmm语音模型已经介绍完了。可以用来做语音合成，语音识别。但是，这种简单的模型还不够鲁棒，不够完善。后面介绍的context-dependent模型，状态绑定，duration模型，GMM，stream是为了提高鲁棒性。输出模型GV，F0是语音合成方面需要处理的问题。

context-dependent model和状态绑定

上文介绍的都是基于单音素的模型（monophone），即每个音素对应一个hmm。这样无法反映每个音素在不同的上下文环境中发声情况不同。所以一般使用双音素模型（biphone）， 三音素模型（triphone） 例子：

考虑到词内、词间的不同，三音素模型的划分又有不同。(可能的优化点，与停顿相关)

现在更常用的是三音素模型，下文默认都是使用三音素模型。 在三音素模型中，需要注意的是这里每个模型（例如B-R-AY）对应的是一个hmm模型，对应三个状态，而不是多个不同的音素模型（B，R，AY）进行拼接。 这样使用三音素模型可以将音素从不同的上下文区分开来。但是也造成了组合爆炸。也就是很多组合可能根本就没出现，或者很少出现，无法对齐进行参数估计。所以，需要引入聚类，将相似的状态进行聚类。需要注意的是，聚类的时候，两个模型分别对应的3个状态）很少一模一样， 很有可能只是部分相同。

下面考虑最简单的绑定：

在HTK中TI表示绑定。上面的例子是将每个模型中间音素相同的第三个状态进行绑定。将设以某个音素为中间音素的模型数的平均数为100。 那么在绑定之前共有300个状态，通过绑定之后则变成201个状态。这种方法虽然减少了状态数，但是不够鲁棒，而且无法解决数据不足的问题。 基于学习的绑定有：基于聚类的绑定和基于决策树的绑定。参见² p153 基于聚类的方式先假设所有模型都互不相同，然后不断合并距离在一定范围内，数量少的模型。 基于决策树的绑定是先假设所有模型属于同一个类，然后通过决策树的问题，不断分裂，最后达到相同叶子节点的模型分作一类，一起训练。

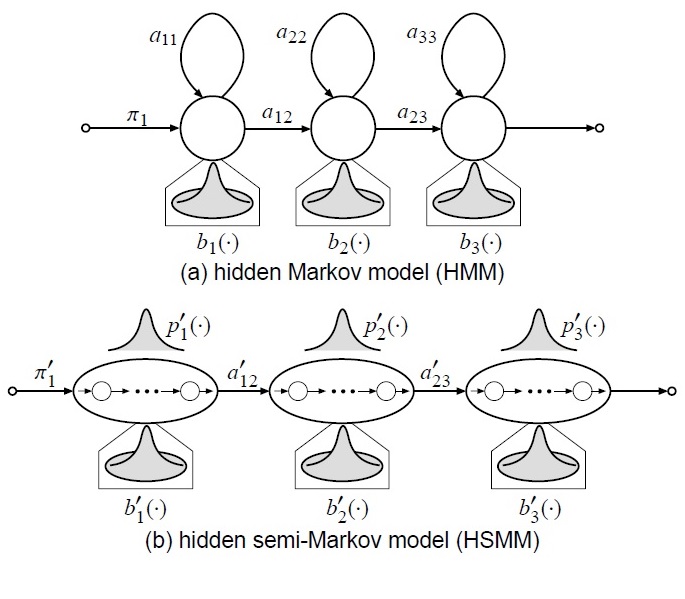
duration模型和hsmm

使用转移模型，使用随机数决定下一个状态是什么，虽然在统计上合理，但是在实际中，很有可能造成剧烈的抖动。实际的声音，往往存在连续性，而且随着时间的增长，同个状态的出现概率呈指数衰减，而不是相互独立的。 一般使用explicit duration model来对duration进行建模。参考⁴

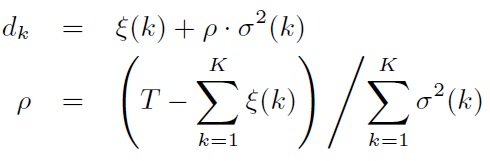
对于给定的合成时间T， 可以求解各个状态的duration: 而上式的ρ可以控制语速。

上面的使用模型的主要问题是explicit duration model只在合成的时候使用，而并没有参与训练。Tokuda等人又提出HSMM，其实就是将explicit duration model加入训练中，获得更好的结果。HSMM与HMM不同之处在于用高斯模型对duration进行建模。公式推导见论文⁵。

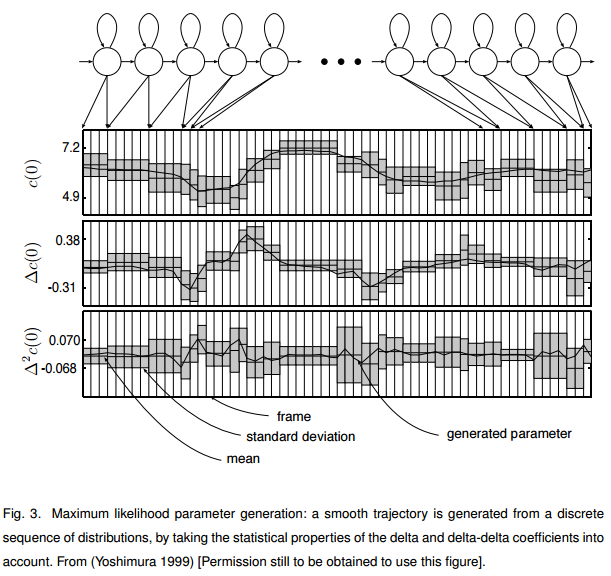
2.3 mlpg gv 参数生成

给定状态到输出参数, 需要额外的处理，否则会使得输出值都是状态的高斯模型的均值，而状态边界又变化太大。参考⁶

mlpg

窗系数矩阵为

\(w_t^{(d)}\)是用于计算第t帧第d阶动态特征的窗系数，只在第t位和相邻位置的元素有非零值，非零值的范围取决于窗宽度，通常为1，即前后一帧。

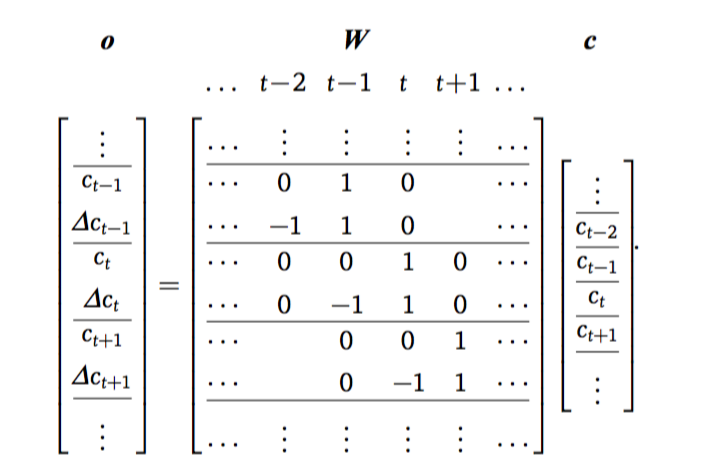
\(I_{M\times M}\)表示\({M}\times M\)单位矩阵，用于将相同的窗系数应用于所有\(M\)维参数。

因此，似然函数表示为

其中

有如下一些定义：

在开始推导参数生成算法之前，我们需要给出线性代数中的一些定理。

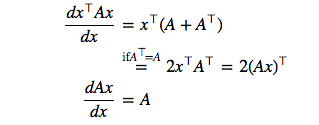
给定高斯分布序列\(q\)，参数生成的准则表示为

在这里，生成的参数序列既是高斯分布的均值矢量序列，生成的语音变化不自然。为避免这个问题，引入动态窗系数作为约束(Tokuda et al., 2000)。在这个约束条件下，以o为变量的函数最大化就等价于以c为变量的函数最大化。

根据多变量高斯密度函数的定义，得到

似然度定义为密度函数的自然对数。对似然函数求c的偏导数得到

令$\frac{\partial\log\mathcal{N}(Wc_{max}\mid \mu_{q},\Sigma_{q})}{\partial c_{max}}=0,$可得以下等式

可以得到如下线性方程（组）

其中

通过求解方程（组）即可得到极大似然准则下的参数序列。

使用Cholesky 分解，$R_{q}$可以表示为

其中$U_{q}$是一个上三角矩阵。因此参数求解方程（组）可以分解为两个方程（组）

上述方程组可以通过前向-后向迭代法（高斯消去法）求解。

mlpg gv参数生成

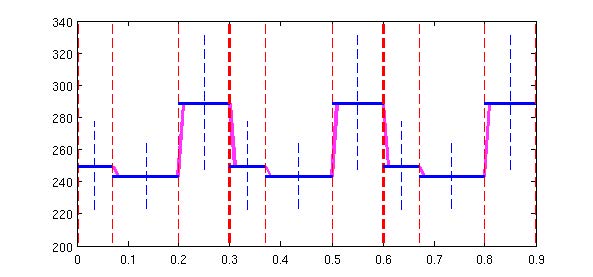
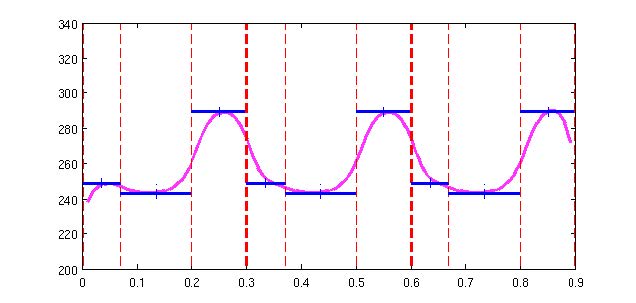
从下图中可以看出，自然语音和合成的语音对比差异：从频率域坐标和能量域坐标方向看出，自然的变化幅度更明显，而合成的语音过度平滑。

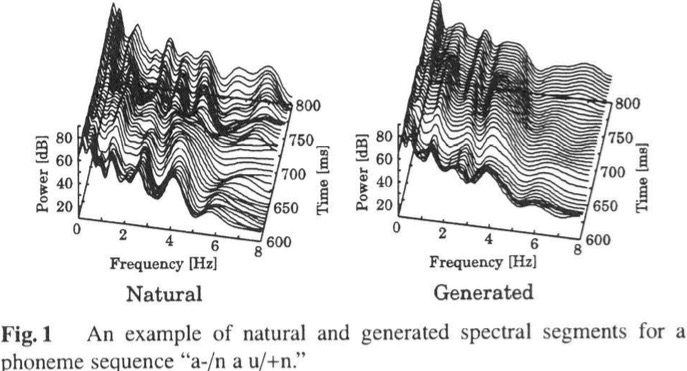
在时刻第t帧的参数由矢量表示为

以及一个T帧的静态特征向量为

GV定义为各阶静态特征参数在T帧内的方差，如下列三个公式：

过程如下：在训练阶段，首先从训练语句汇总统计GV值，每个训练语句得到一个GV向量，之后用这些GV样本来估计GV模型参数，以下是用一个单高斯分布来表示GV模型,公式12转化为如下公式：

w为权重，用于平衡这两个似然值。求解特征参数序列C的值，使得输出概率logL值最大；

我们使用梯度下降法来更新C值：

对L求导，得到如下公式： \(\begin{aligned} \frac{\partial{L}}{\partial{C}}=\omega\left(-W^{\top}U^{-1}WC+W^{\top}U^{-1}M \right) +\left[\acute{v_1}^{\top},\acute{v_2}^{\top},\ldots,\acute{v_T}^{\top}\right]^{\top},\\\\ \acute{v_t}=\left[\acute{v_t}(1),\acute{v_t}(2),\ldots,\acute{v_t}(d),\ldots,\acute{v_t}(M)\right],\\\\ \acute{v_t}(d)=-\frac{2}{T}p_v^{(d)}\left(V(C)-\mu_v\right)\left(c_t(d)-\overline{c}(d)\right), \end{aligned}\)

则可得下列公式

该方法建立一个GV模型用来刻画语音参数轨迹在整句级别上的变化程度。生成的语音参数最大化由HMM似然值和GV似然值构成的一个似然函数。GV似然值用来惩罚所生成的语音参数轨迹的整体方差的降低。

2.4 声码器

常用的声码器有MLSA,STRAIGHT, WORLD等。下面介绍world中D4C算法。

2.4.1 参数定义

D4C算法使用基于组延迟的参数,该参数从基本周期为T0的任意周期信号形成F0Hz的正弦波。因此，正弦波与其他频率分量之间的功率比对应其非周期信息。

周期信号定义

定义声音信号\(y(t)\)由一个脉冲响应\(h(t)\)和一个基本周期为T0的脉冲信号的卷积得到。信号\(y(t)\)及其频谱\(Y(\omega)\)由下式表示：

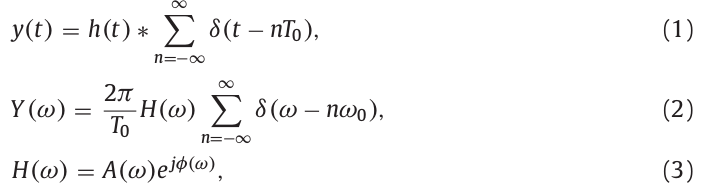
其中，\(\omega_0\)表示基本角频率（\(=2\pi/T_0\)），\(A(\omega)\)和\(\phi(\omega)\)分别表示信号的幅度谱和相位谱。频谱\(Y(\omega)\)由基本分量和谐波分量组成，对频谱\(Y(\omega)\)，用幅度\(\alpha_n\)和相位\(\beta_n\)归一化得到：

实际语音中，非周期分量为噪声成分，非周期信息为语音信号与非周期分量之间的功率比，而这个功率比取决于频带，所以非周期信息为在多个频带上的功率比。算法中取5个频带的非周期信息。

基本方程定义

组延迟参数\(\tau_g(\omega)\)定义为基于相位\(\phi(\omega)\)的频率导数:

组延迟用另一种方法表示为：

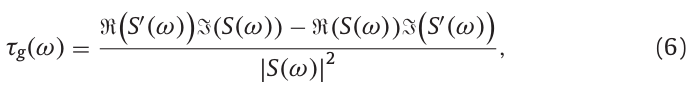
其中，\(S(\omega)\)表示输入信号\(s(t)\)的频谱,\(S'(\omega)\)为信号\(-jts(t)\)的频谱，即：

D4C算法使用式(6)进行计算，基于组延迟的时间静态参数用于非周期信息估计，在式(6)中的分子和分母中使用。

2.4.2 D4C算法步骤

在周期信号分析中，窗口波形及其频谱取决于窗的时间位置。用时间静态表示频谱包络对高质量的语音合成非常重要，同时对非周期信息估计也很重要。

D4C算法使用基音同步分析来设计窗函数和基于组延迟的时间静态参数。D4C算法由以下三个步骤完成：

第一步：计算基于组延迟的时间静态参数

对式(6)的分子用\(E_{cs}(\omega)\)表示：

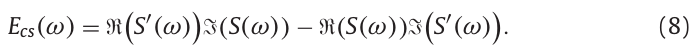
假定由\(E_{cs}(\omega)\)周期信号\(y(t)\)计算得到，由式(2)知，周期信号\(y(t)\)具有在频率\(n\omega_0\)上的谐波分量，且每个谐波分量有不同的幅度和相位。因此对窗函数的设计需符合下面两个要求：

（1）主瓣宽度为\(\omega_0\)。

（2）旁瓣幅度远低于主瓣幅度。

信号\(y(t)\)在窗函数中心位置为\(\tau\)处的频谱表示为：

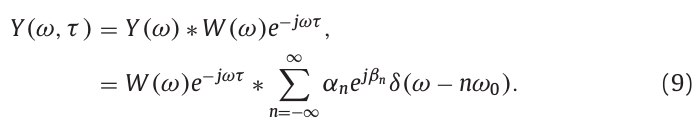
\(Y(\omega,\tau)\)在\(n\omega_0\)处具有谐波分量，经过卷积窗函数后，谐波\(k\omega_0\)被限制在\((k-1)\omega_0\)到\((k+1)\omega_0\)频率范围。由于窗函数的作用，我们可以只计算相邻分量\(k\omega_0\)到\((k+1)\omega_0\)之间的干扰影响。下式以k=0的情况进行解释：

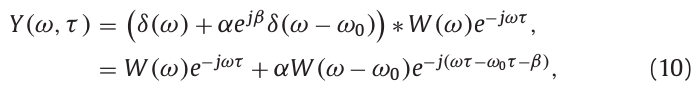
其中，\(W(\omega)\)为窗函数的频谱，\(\alpha\)和\(\beta\)分别是振幅\(\alpha_1\)和相位\(\beta_1\)，\(\alpha_0\)和\(\beta_0\)分别被归一化为1和0。

为了消除时变分量\(\tau\)，插入参数C：

上式用\(Y_0(\omega,\tau)\)作为\(Y(\omega,\tau)\)的频率导数。这里假设\(W(\omega)\)没有虚部，且关于时间对称，范围从-N/2到N/2，窗宽度为N。\(Y(\omega,\tau)\)和\(Y_0(\omega,\tau)\)的实部和虚部用于计算\(E_{cs}(\omega,\tau)\)。

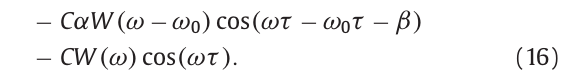
上式各项代入式(8)得到：

式(11)的傅里叶变换，经过窗函数，时间位置\(\tau\)，其积分范围被限制在\((\tau-N/2,\tau+N/2)\)，由于参数C对应于时间偏移，积分范围变为\((\tau+C-N/2,\tau+C+N/2)\)。如果要固定积分范围为\((\tau_0-N/2,\tau_0+N/2)\)，则参数C被自动设置为\(-\tau+\tau_0\)，得到下式：

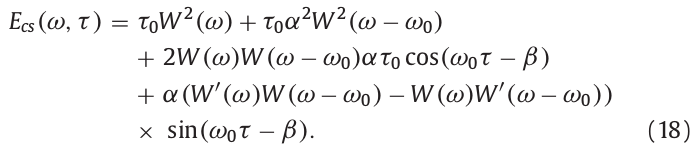
上式中，\(\tau_0\)可以被设置为与时间位置\(\tau\)无关的任意值，参数C被自动设置为用于消除时间位置\(\tau\)的值。因此式(18)的第一和第二项在时间上是静态的。通过正余弦的性质，可以消除第三第四项，即将时间中心位置移置\(\tau\)，得到：

\(E_D(\omega,\tau)\)是用作式(6)分子的参数。\(E_D(0,\tau)\)和\(E_D(\omega_0,\tau)\)分别为\(2\tau_0 W^2(0)\)和\(2\tau_0\alpha^2W^2(0)\)。上式只是k=0的结果，递推到任意k值如下：

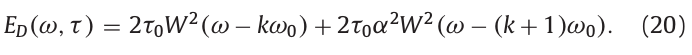
接下来计算式(6)的分母，总功率谱。用窗长度为\(\omega_0\)的矩形窗对在时间位置\(\tau\)的功率谱进行平滑，得到：

通过式(20)和式(21)，可以计算基于组延迟的时间静态参数：

上式分子和分母在时间位置\(n\omega_0\)处的值相同,即基于组延迟的时间静态参数在所有谐波分量上的值相同。这意味着式(22)对具有相同F0的任意信号输出相同的结果。

第二步：参数成型计算

在第一步中，计算基于组延迟的时间静态参数\(\tau_g(\omega,\tau)\)，第二步则式对时间静态参数进行转换，得到用于第三步计算的参数。

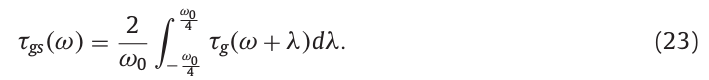
图2中，对时间静态参数\(\tau_g(\omega)\)依次用不同长度(长度分别为\(\omega_0/2\)和\(\omega_0\))的窗进行平滑，然后对两次平滑后的结果相减得到一个周期为\(\omega_0\)的正弦波信号。

\(\tau_D(\omega)\)为用于第三步骤计算的参数。由此。我们可以从任何周期信号中获得频率为ω0的正弦波。去除噪声分量的正弦波的功率被用于估计非周期信息。

第三步 估计频带非周期信息

频带非周期信息通过每个频带的总功率与拟合得到正弦波的功率之间的比值得到。因此D4C算法可以估计具有特定频带中心频率的频带非周期信息。

在D4C算法中，Nuttall窗口作为具有低旁瓣的窗函数被使用。旁瓣比主瓣低90 dB，并且窗函数比Blackman窗更好。使用窗函数\(W(\omega)\)移位中心频率到\(f_c\)，对参数\(\tau_D(\omega)\)进行加窗。 \(\omega_c\)是角频率并且等于\(2\pi f_cHz\)。使用傅里叶逆变换计算波形 \(P(t,\omega_c)\)。

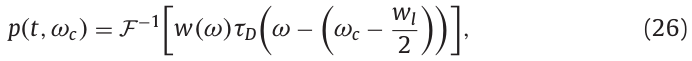
其中，\(\omega_l\)为窗函数的长度。

$p_s(t,\omega_c)$表示对式(26)得到的功率波形$\mid p(t,\omega_c)\mid^2$，将归一化总功率为1后进行排序。

最终计算得到在角频率\(\omega_c\)上的非周期信息：

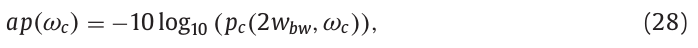
式中，\(w_{bw}\)表示窗函数的主瓣带宽，为时间位置。主瓣带宽被定义为从0Hz到振幅为0的最短频率范围。上式主瓣带宽位置设置为\(2w_{bw}\)。

3 基于深度学习的参数语音合成

基于hmm的三音素聚类的语音合成方式存在着局限性。hmm本身在假设状态之间条件独立，不符合实际情况，而且，hmm通过构造问题集进行三音素聚类，非常依赖问题集的质量。这增加了调参的难度。基于深度学习的方法很大程度上避免了这种局限性。

基于深度学习的参数语音合成框架与基于hmm的参数语音合成大体类似。文本特征提取以及声码器部分是通用的。不同部分在于文本特征到声学特征的模型建立。可以采用不同的深度学习方法进行建模: dnn, rnn。

以下通过以下几个方面来阐述深度学习语音合成的细节。

• 时长模型
• 声学模型
• 预测
• 网络模型，dnn，rnn等

下文假设每个音素提取的文本特征是546维。文本特征构造详见2.1

3.1 时长模型

时长模型学习文本特征到五个状态帧数的映射。

输入特征: 546维文本特征

输出特征: 5维时长, 5状态对应的帧数。

训练数据的5维时长特征通过自动对齐的方式获得。可以用htk，kaldi等工具对声音数据对齐。确定每个音素对应的五个状态的帧数是多少。

3.2 声学模型

声学模型就是要学习文本特征到声学特征的映射。

现在比较好的开源声码器是world。world将48k的wav每帧分解成以下声学特征: 60维mgc，5维bap，1维f0。声码器可以使用以上声学特征重构出wav。

深度学习训练需要构造文本特征到声学特征一一对应数据对。一个音素一般对应多帧声学特征。需要对文本特征进行扩充。常用的扩充特征有：

• 当前状态类别
• 当前帧到当前状态开头的百分比
• 当前帧到当前状态结尾的百分比
• 当前帧到当前音素开头的百分比
• 当前帧到当前音素结尾的百分比
• …

输入特征: 546维文本特征 + 上述9维扩充特征

输出特征: 60维mgc特征(x3) + 5维bap特征(x3) + 1维度lf0(x3) + 1维vuv特征。共199维。

之所以乘以3，是包含了delta，delta delta特征。在合成的时候需要使用mlpg进行平滑。后面在预测部分会加以解释。

接下来我们介绍一下这个vuv是什么？

3.2.1 vuv

vuv特征是dnn相对hmm特征独有的。vuv是voice，un voice的缩写。也就是说，这一维用来表示是否有发生。在训练的时候，通过是否提取到f0来判定是否发音。

具体规则如下:

• 如果提取到f0，则vuv设置为1，f0的值取为提取到的f0
• 如果没有提取到f0，则vuv设置为0，f0使用插值数据

3.2.2 归一化

时长模型和声学模型的归一化方式: 输入归一化到0.01~0.99, 输入使用mvn归一化。

3.3 预测

上面讲的是训练。下面讲预测，我们用具体的例子将以上东西穿起来。

假设有一个一句话: 欢迎使用语音合成服务。

• 前端文本分析
  • 总的10个字，假设我们将其分解成20个音素。
  • 通过前端文本分析，我们可以获得20x546的时长模型输入特征。
• 时长模型
  • 将这个时长输入特征输入到时长模型，获得20x5的时长特征
• 声学模型
  • 使用20x5的时长特征对20x546的特征进行扩充，获得1215 x 555的声学模型输入特征
  • 将1215x555的特征输入声学模型，获得1215x199的声学特征。
• 声码器
  • 使用mlpg平滑，根据delta，delta delta获取符合约束的60维mgc，5维bap，1维f0
  • 根据vuv这维输出，将vuv值小于某个阈值(0.6)的f0置为0. 这个阈值可以调整
  • 将mgc，bap，f0合成声音

3.4 网络模型

3.4.1 dnn

使用6层mlp。每层256，512，1024节点均可。采用tanh激活函数。

3.4.2 rnn

一般比较好的模型是基于双向lstm的。可以通过拼接多帧来加速预测。

4 adapt技术

4.1 基于HSMM的MLLR

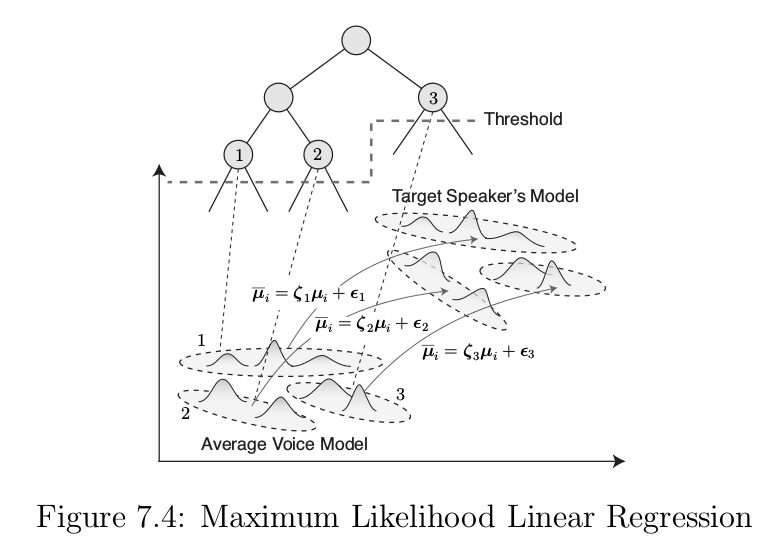
最大似然线性回归(MLLR)是一种基于仿射变换的方法，该算法假设原模型的参数与自适应后的模型参数之间存在线性关系，利用少量自适应数据，根据最大似然准则估计一个线性的转移矩阵，将原模型参数映射为新的模型参数，使得在新的模型参数下出现新观察向量的似然概率最大。MLLR主要对高斯密度函数的均值向量进行自适应，其他参数在自适应模型中不做改变。

MLLR通过平均音模型的状态输出均值向量和时长分布，线性转换为目标说话人的状态输出均值向量和时长分布：

其中，\(\mu_i\)和\(m_i\)分别表示平均音模型的状态输出均值和时长分布均值。L为观察向量的维度，d为时长。状态输出均值向量 的转换矩阵为： 时长分布的均值向量 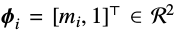的转换矩阵为：

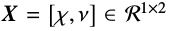
估计变换参数\(\wedge=(W,X)\)即最大化自适应目标说话人观察向量O（长度为T）的似然值：

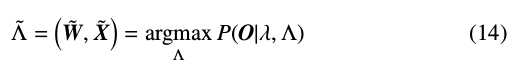
利用Baum-Welch方法重估计变换参数：

其中：(\(l\)表示第\(l\)个行向量)

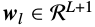
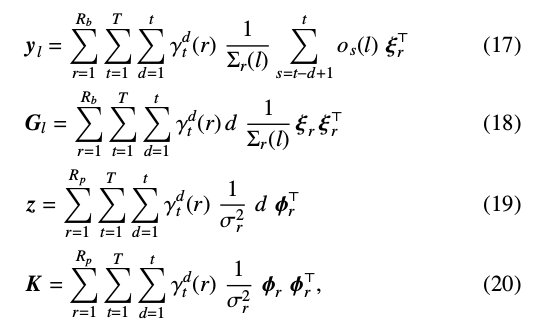
这里：$\xi_r$表示状态r的输出概率均值向量，$\Sigma_r(l)$表示状态r的协方差矩阵$\Sigma_r$第$l$个对角元素，$\phi_r$表示状态r时长均值向量，$o_s(l)$表示观察向量\(o_s\)的第\(l\)个元素。

由于目标说话人风格的自适应数据量有限，因此对每个分布未必都能估计W和X。所以，利用树结构将模型中的分布进行分组，并将变换矩阵与组进行关联。式（17）-（20）中，$R_b$和\(R_p\)分别表示属于同组的状态输出和时长分布的分布数目。

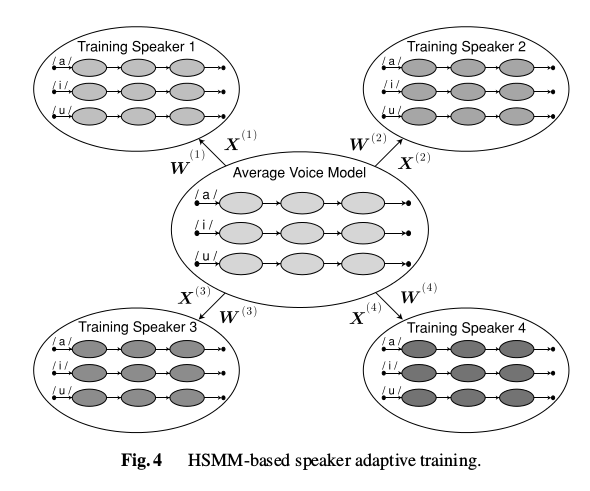
4.2 平均音模型（Average Voice Model）

如图1所示，整个说话人自适应训练语音合成系统是在传统的说话人相关训练模型的基础上加入说话人自适应训练，首先利用多个说话人的语音数据获得一个平均音模型，在利用目标说话人少量语音数据做自适应训练，得到自适应目标说话人的HMM，然后合成出目标说话人的语音。

平均音模型：在HMM语音合成训练过程中，分别对语音库中每一个说话人的语音数据进行训练，利用得到的每个音素HMM模型，做概率分布统计和决策树聚类得到的平均音的hmm模型。

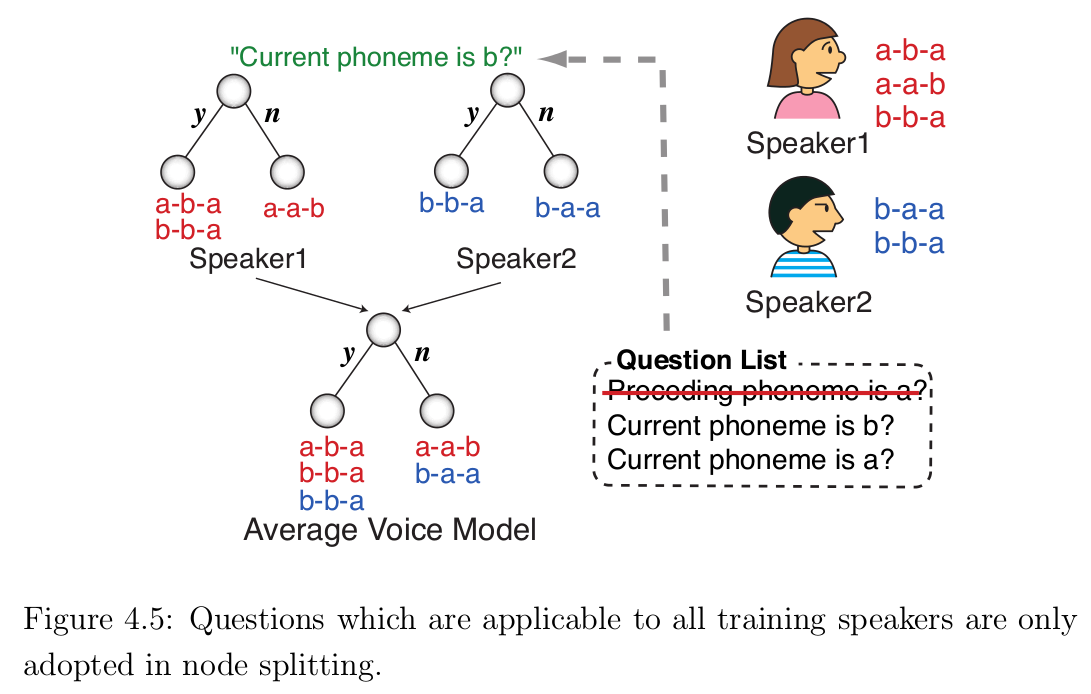
4.3 说话人自适应训练（SAT）

为了在目标说话人自适应中提高合成语音的音质，需要归一化训练说话人之间的差异性和相关性，因此提出一种说话人自适应训练算法来消除训练说话人之间的相互影响。

在说话人自适应训练中，训练说话人的训练语音数据和平均音之间的差异用一个输出状态分布均值向量和时长分布的线性回归函数表示。利用一组状态输出分布和状态时长分布的线性回归方差归一化训练说话人之间的差异：

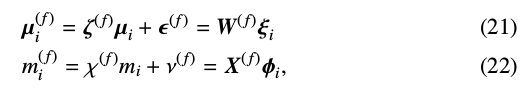
其中，\(\mu_{i}^{(f)}\)和\(m_{i}^{(f)}\)分别表示训练说话人\(f\)的状态输出均值向量和时长分布。

F个训练说话人的训练总数据为\(O=\{O^{(1)},...,O^{(F)}\}\)，\(O^{(f)}=\{o_{1_f},...,o_{T_f}\}\)为训练说话人\(f\)(长度为\(T_f\))的训练数据。

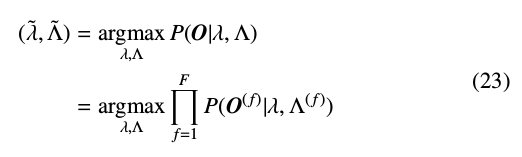
4.4 dnn adapt

可以分别在特征输入使用ivector扩展，在层

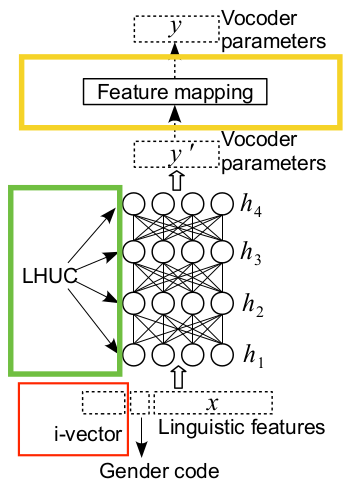
4.4.1 ivector提取

ivector能够很好地表示每个说话人的特点，被广泛引用与说话人识别，对语音识别也有促进作用。

其中$s$是提取的ｇｍｍ特征。$m$是UBM模型的平均向量。$T$是方差。$i$就是所求的ivector向量。

4.4.2 ihuc

学习每个隐含层单元的贡献。

其中:

• $h_m^l$是第$l$层的激活值
• $\alpha(r_m^l)$是位乘运算以限制$r_m^l$的取值范围
• $w^l$是第$l$层隐含层的权值
• 设置$\alpha(r_m^l)=1$, 则是普通神经网络

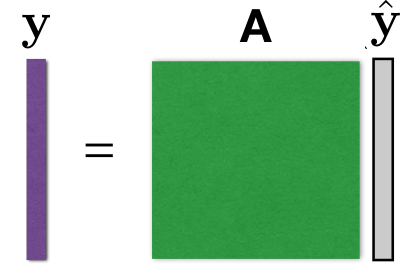
4.4.3 feature space map

学习转换参数，获得特征之间的映射。

５ 基于生成模型的语音合成

wavenet

与传统的声音合成不一样，wavenet不需要经过声音特征参数的抽取或者生成就能直接合成出声音。也就是wavelet不需要生成mfcc，mgc等声音特征参数，然后再经过声码器（共振峰，straight等）合成声音;其输入是前一时刻音频波形数据(wav文件读取后的16位short类型数据)，输出是下一时刻的音频波形数据。

wavenet在没有额外信息作为输入的情况下，所生成的音频内容是不可懂的。但在给定额外信息，如语音合成系统（TTS）中的文本特征和f0等信息，wavenet能够生成干净，非常自然的语音。

5.1 wavenet

wavenet的所有操作都是由一维卷积操作构成。由基本的一维卷积操作构建出 考虑上一时刻输入信息的causal convolutional layers（causal：因果），再由causal convolutional layers构建出以考虑更前时刻并减少参数的dilated causal convolutional layers（dilated：加宽，膨胀）。最终由dilated causal convolutional layers， gated activation unit和 residual and parameterised skip connections构建出wavnet。下图为整个wavenet的结构。

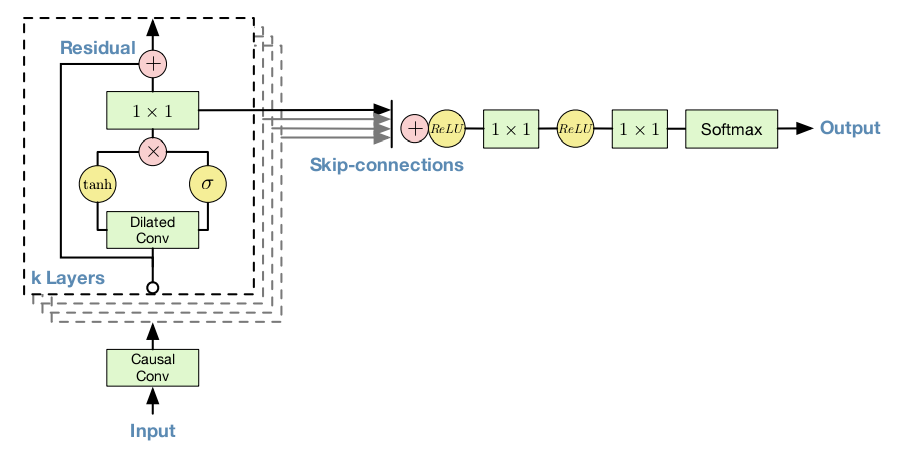
图中虚线框代表一个dilated causal convolutional layer，里面包含了一个gated activation unit，其输出分别是Residual和Skip-connections。其中Residual作为下一层dilated causal convolutional layer的输入，而当层的Skip-connections输出将会同其他dilated causal convolutional layer的Skip-connections求和后作为最后wavenet的两层一维卷输出层的输入。

5.2 Causal Convolutional Layer

Causal Convolutional Layer 是一个滤波器的滤波宽度为2的一维卷积层。一维卷积中的滤波器有三个参数，分别是滤波宽度，输入数据通道数，输出数据通道数。滤波宽度表示滤波器作用在输入时间序列的有效时长，在因果卷积中为2,意思是有效时长是当前时刻和前一时刻的输入数据。输入数据通道数与输出数据通道数，类似于二维卷积中的输入特征图数，和输出特征图数。事实上，一维卷积操作是在二维卷积操作上实现的。下图为一个多层的因果卷积网络，每个圆圈表示一个时刻的数据（非时序数据中的一个样本）。

5.3 Dilated Causal Convolutional Layer

为了时wavenet由更大的感受野同时减少参数，论文中使用了一种叫dilated causal convolutional layers。dilated的意思是，一个滤波宽度为二的一维卷积中，其所卷积的目标不再是当前时刻和前一时刻的输入数据，而是当前时刻和跳过了中间的若干时刻的输入数据。具体如下图所示：

5.4 Gated Activation Unit && Residual and Skip Connections

为了更好的学习出复杂数据规律，论文加入了Gated Activaton Unit，有点类似于LSTM中的各种门。在没有使用Gated Activation Unit之前，每层的Dilated Causal卷积层都只一个Dilated Causal卷积操作,再经过tanh函数。而在使用之后，每层Dilated Causal卷积层多一个经过sigmoid函数的Dilated Causal卷积操作，共同构成Gated Activation Unit。具体公式如下：

Residual 和 Skip Connections 则是在dilated Causal卷积操作后加入两一维卷积操作，分别得到Residual和Skip输出。

5.5 音频数据量化

wavenet的声音生成，是当作一个分类问题，而不是回归问题。对于16位的音频数据有65536种可能，这样一来网络的输出就会非常大。为了简化输出，论文使用了u-law编码算法将16位压缩为8位，最终的网络输出为256。u-law压缩与解压缩如下：

编码: $F(x)=sgn(x)\frac{ln(1+u\mid x\mid)}{ln(1+u)},-1 \leq x \leq 1$

解码:$x=sgn(F(x))\ast (1/F(x))\ast ((1+u)^{\mid F(x)\mid}-1)$

其中，$u=255(8bit)$

5.6 wavelet在TTS中的应用

wavenet在用来语音合成时，将文本特征，时长以及f0作为额外信息作为输入。由于这些额外信息是对应音频的每一个帧的，因此需要将这些特征上采样到一个采样点的级别。例如，假设有10s，16000Hz的音频，将其分成1000帧。假设已经获得了文本特征，时长以及f0等信息，那么这些信息也会有1000帧。而10s的音频共有16000×10个采样点，因此需要将1000帧的额外信息上采样到16000×10。论文中是用一个额外的卷积神经网络作为上采样器。得到上采样后的额外信息后，将这些信息作为每一层dilated causal卷积层的另外一个输入，这样就构成了一个TTS系统了。

char2wav

sampleRnn